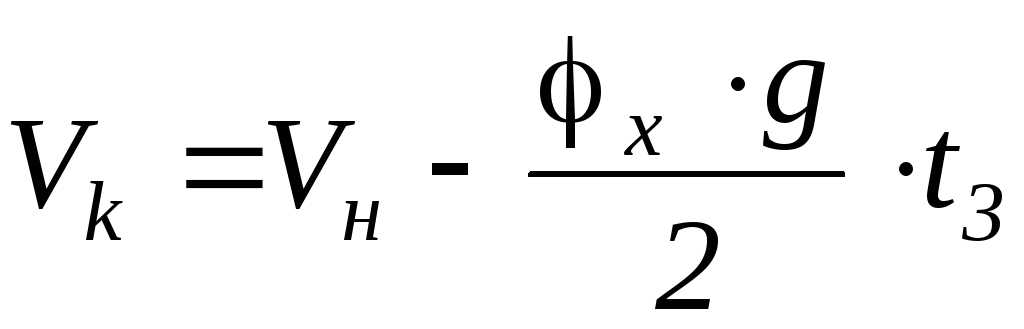Силы действующие на автомобиль при торможении – 12 Тормозная динамика автомобиля и ее значение для безопасности движения. Требования к тормозным системам.
- 18.05.2020
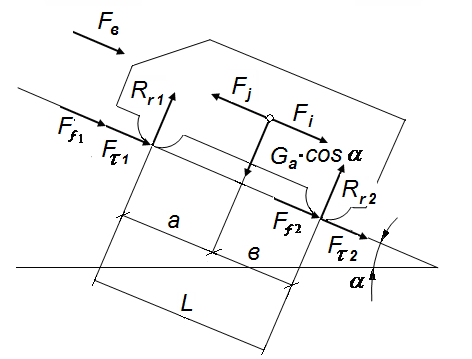
4.3. Силы, действующие на автомобиль при торможении (общая схема)
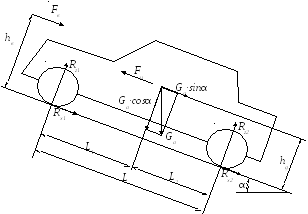
Тормозной баланс автомобиля:
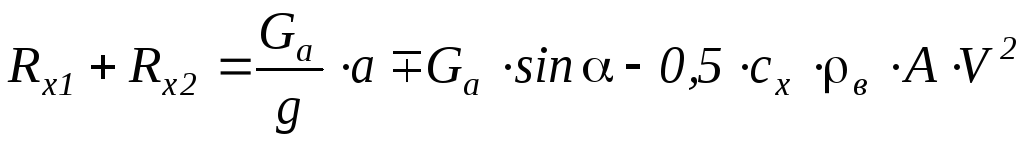 .
.
Найдем тормозные моменты:
Продольные реакции на колесах при отсоединенной трансмиссии:
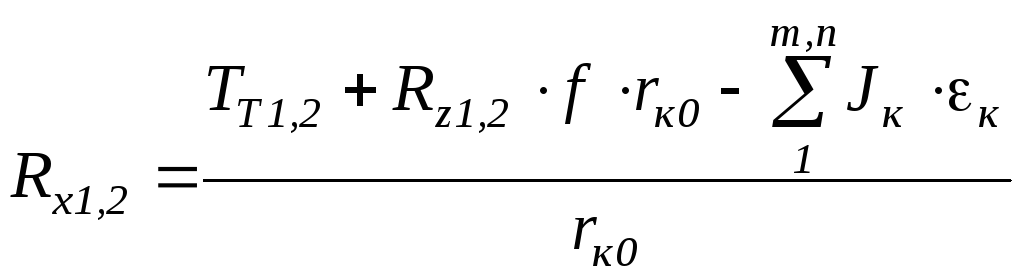
Тормозной момент двигателя:
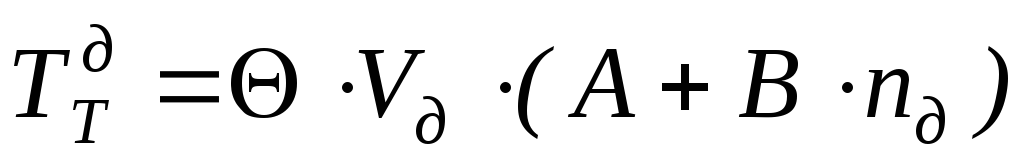 ,
Н · м,
,
Н · м,
где Θ, А, В – эмпирические коэффициенты; Vд – объем двигателя, л; nд – скорость двигателя, об/мин.
Двигатель | Θ | А | В |
Бензиновый | 12,5 | 0,4…0,5 | 0,0035 |
Дизельный | 15 | 0,5…0,7 | 0,005 |
При 1000 об/мин ТТ = 80 (V=1,6 л). При 5000 об/мин ТТ = 360.
5–7 кВт/л (Справочник Бош, с. 649)
Подведенный к полуоси тормозной момент двигателя:
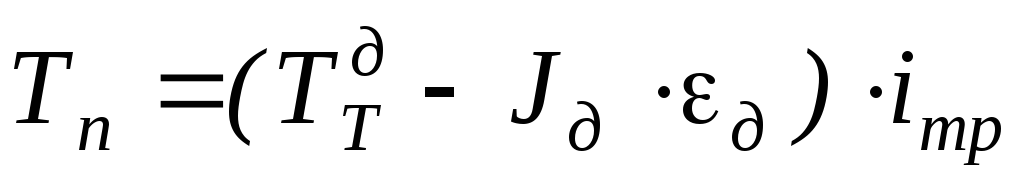 ,
,
где Jд – момент инерции двигателя; εд – ускорение двигателя; iтр – передаточное число трансмиссии.
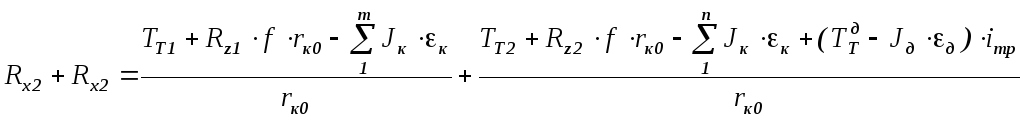 .
.
Перегруппируем тормозной баланс автомобиля, перенеся в правую часть силы, останавливающие автомобиль, а в левую – вызывающие его движение:
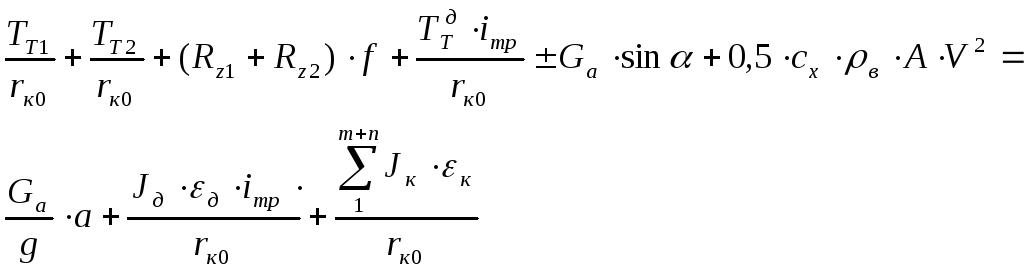
Введем замену в
правой части: 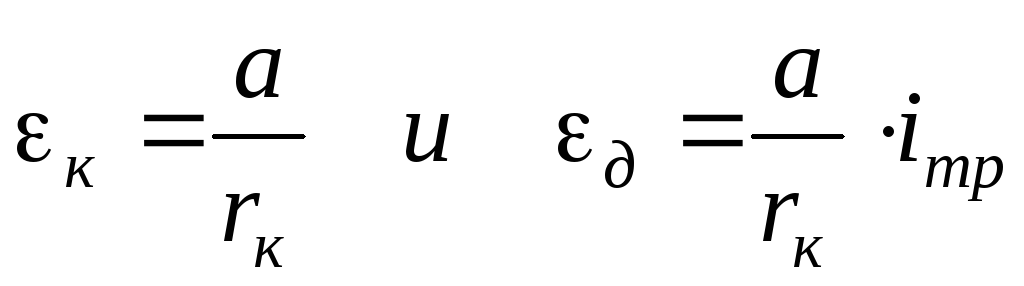 .
.
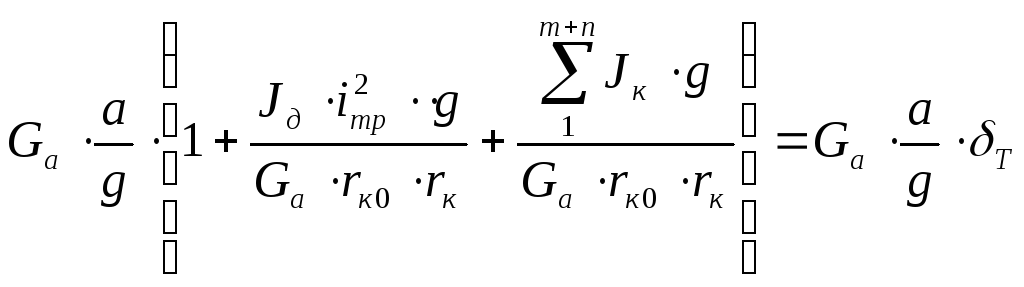 .
.
По аналоги с коэффициентом учета вращающихся масс при разгоне запишем:
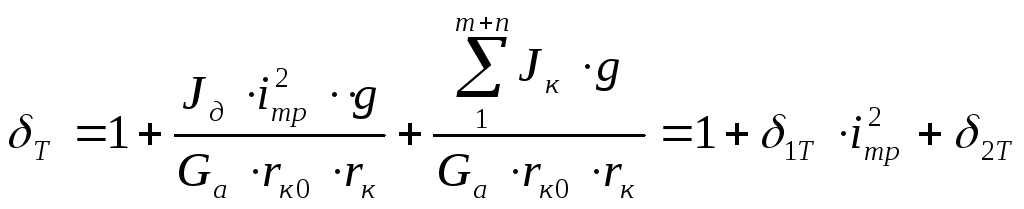 .
.
Примечание:
Отличие (от δ разгона) –произведение радиусов (замена кинематического радиуса статическим приводит к существенной ошибке в расчете).
Введем дорожное сопротивление:
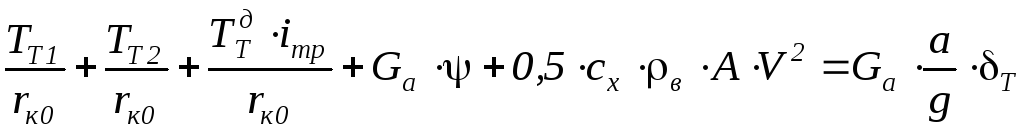 .
.
Найдем замедление автомобиля
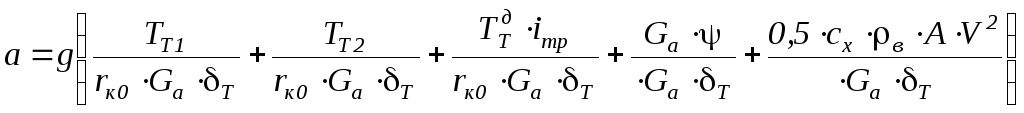 .
.
4.4. Торможение юзом
При торможении автомобиля с блокировкой колес (юзом) отсутствует вращение колес, следовательно, тормозной баланс определим следующим образом:
ma · a = Rx1 + Rx2 +/– Ga · sin α +0,5 · Cx · ρв ·
Rx1 + Rx2=Ga · φx · cos α
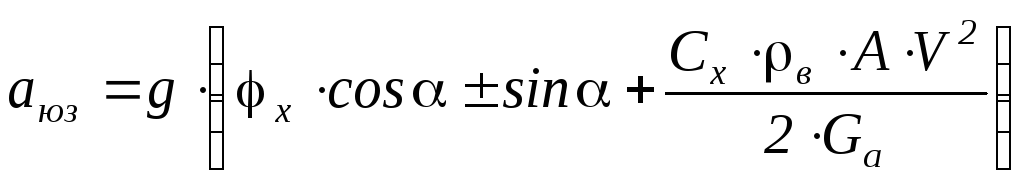 .
.
Если тормозим на горизонтальной площадке, то:
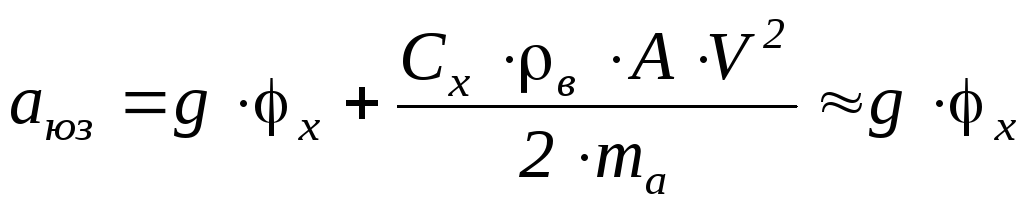 .
.
Пример: Ga=14560 Н; φx = 0,8; Сх = 0,48; А = 2,4 м2; V = 30 м/с Найдем начальное замедление, с которым движется автомобиль в момент попадания колес в юз:
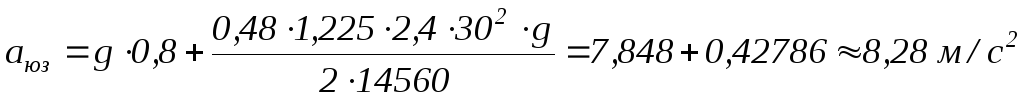
если провести
расчет для влажного асфальта ( коэффициент
сцепления при юзе около φx = 0,4), то 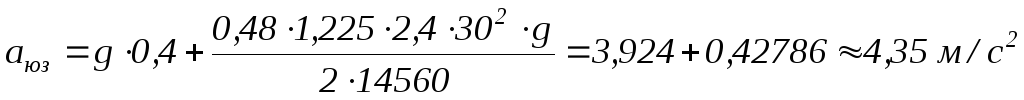
Замечания:
Аэродинамическая составляющая замедления является функцией квадрата скорости и поэтому быстро уменьшается по мере снижения скорости.
Доля аэродинамической составляющей замедления уменьшается по мере увеличения массы автомобиля.
Коэффициент сцепления сильно зависит от относительного скольжения
При юзе всех колес развесовка автомобиля не имеет значения!
4.5. Основные показатели процесса торможения
4.5.1. Время торможения:
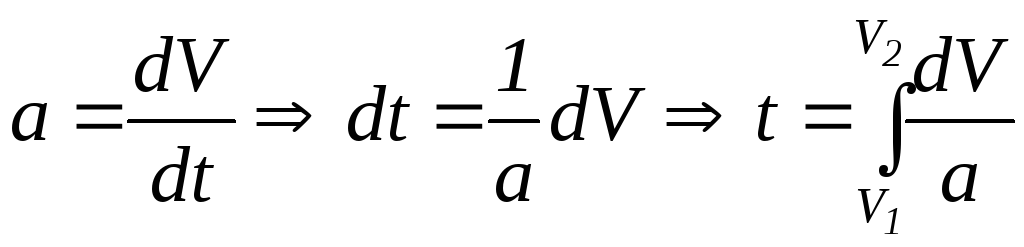
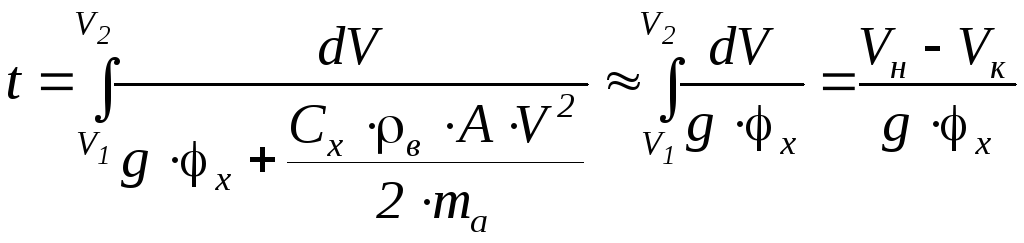
Аэродинамическим сопротивлением часто пренебрегают.
4.5.2. Тормозной путь:
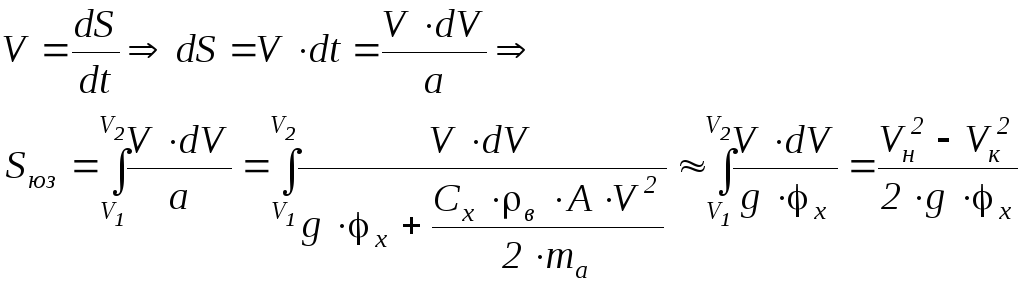 .
.
Если Vк= 0, то 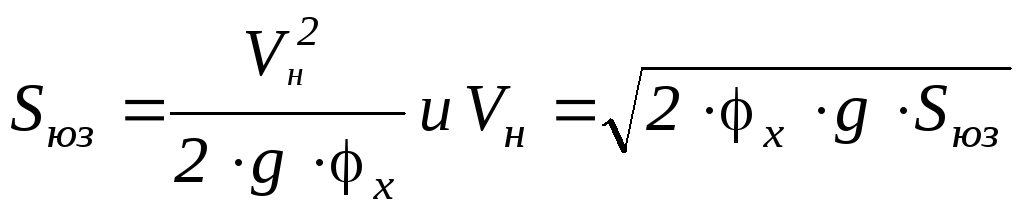
4.5.3. Тормозная диаграмма
t1 – время реакции водителя (в среднем – 0,8 с, но иногда до 1,2 с),
t2 – время срабатывания тормозов (подвод колодок 0,1…0,4 с)
t3 =0,2…0,4 (гидр…пневм)– время нарастания давления в тормозной системе (на этом этапе можно в первом приближении принять линейным закон нарастания давления в тормозном приводе. Это означает, что и замедление автомобиля также нарастает по линейному закону. С точки зрения выходных параметров принимаем a = φ·g/2)
t4 – время торможения t
Найдем остановочный путь:
S1=Vн · t1
S2=Vн · t2
 ,
где
,
где 
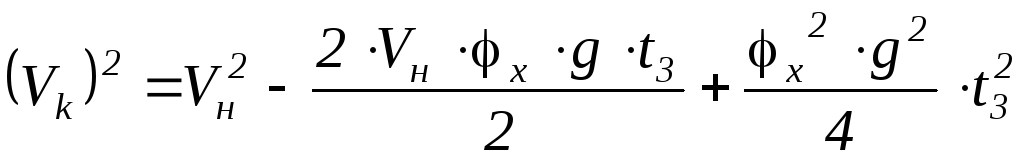
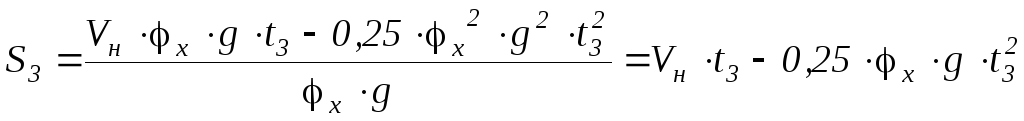
В итоге получим:
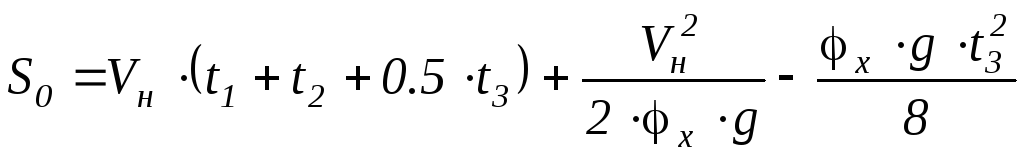 .
.
На практике последним членом пренебрегают:
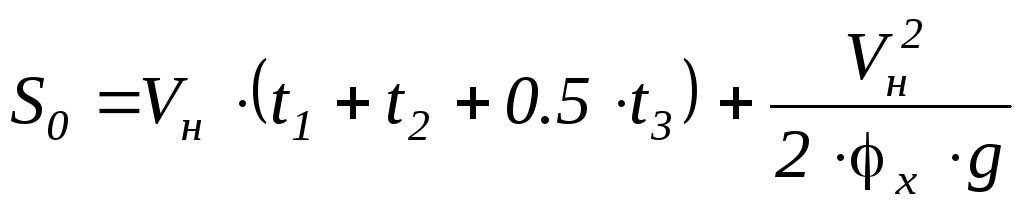 .
.
Пример: V=20 м/c
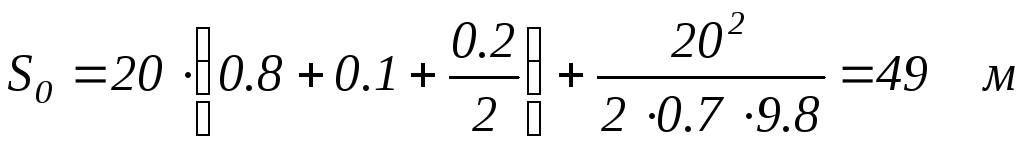
4.5.4. Тормозные силы, моменты, давление в контуре при торможении юзом.
Сила инерции
автомобиля, которой должна противодействовать
тормозная сила:  .
.
Реакции на колесах:
Rx1= Rx1max= Rz1 · φх;
Rx2= Rx2max= Rz2 · φх.
F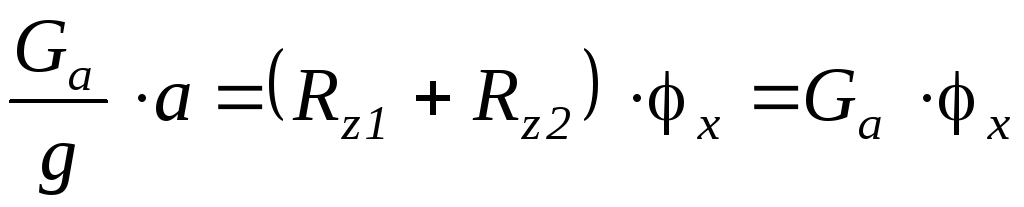 .
.
Определим суммарные нормальные и касательные реакции на осях автомобиля (сопротивлением воздуха и его влиянием на перераспределение нормальных и касательных реакций из-за малости пренебрегаем):
Сумма моментов относительно контакта второго колеса = 0
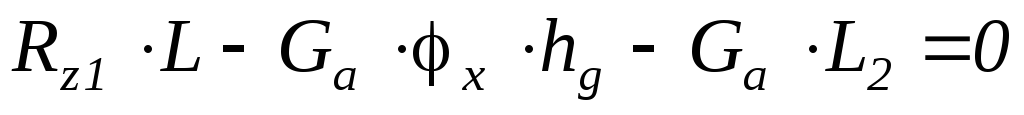 откуда
откуда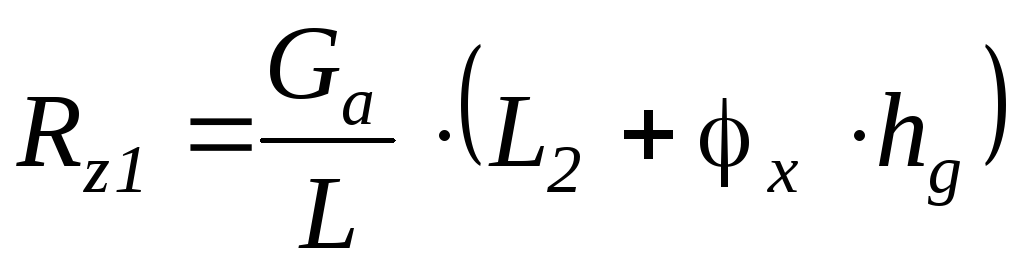
Сумма моментов относительно контакта первого колеса = 0
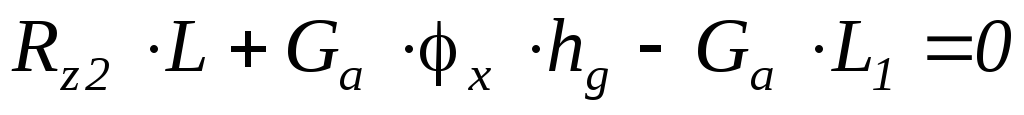 откуда
откуда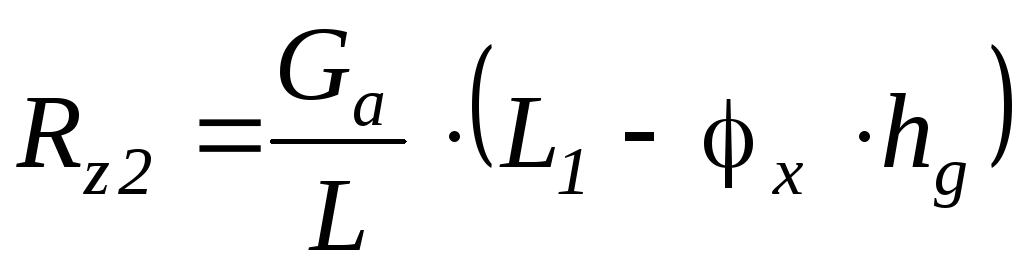 .
.
Откуда: 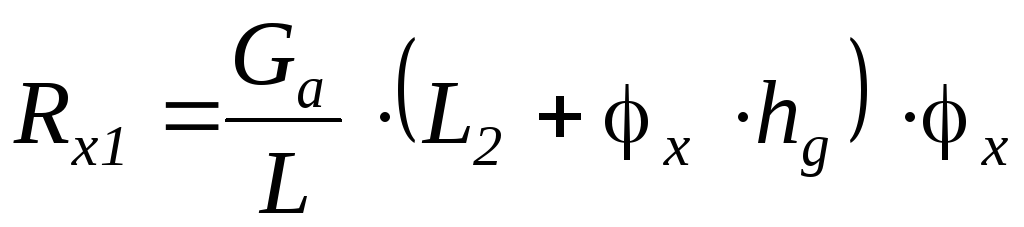

Изменение реакций Rx1 Rx2 Rz1 Rz2 в зависимости от φх
У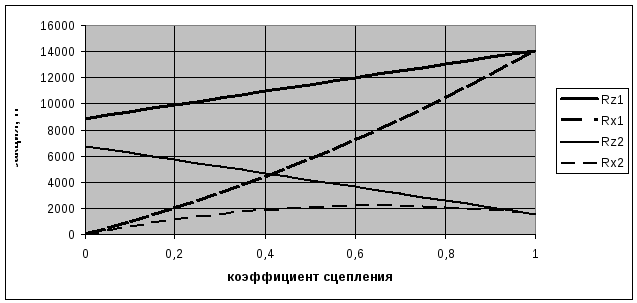 словия
(рис. 1):
словия
(рис. 1):
Ga= | 15600н |
L= | 1,5 м |
L1= | 0,65м |
L2= | 0,85м |
hg= | 0,5м |
Условия (рис. 2)
Ga= | 15600н |
L= | 1,5м |
L1= | 0,65м |
L2= | 0,85м |
hg= | 1м |
Определим необходимый суммарный тормозной момент, который необходимо развить в тормозных механизмах передних колес для доведения их до юза:
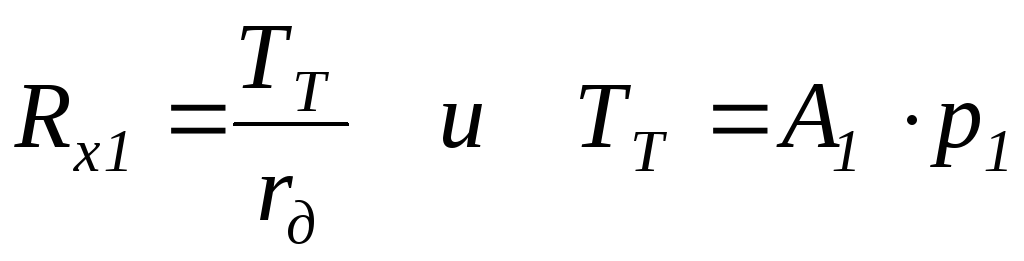 ,
,
где р1 – давление в переднем контуре; А1 – передаточная функция, определяемая конструкцией тормозов (зависимость тормозного момента от давления в контуре). В первом приближении считаем зависимость тормозного момента, развиваемого в исполнительных механизмах от давления в приводе линейной).
Отсюда определим давление, которое необходимо развить в исполнительных механизмах передних тормозов для доведения передних колес до юза:
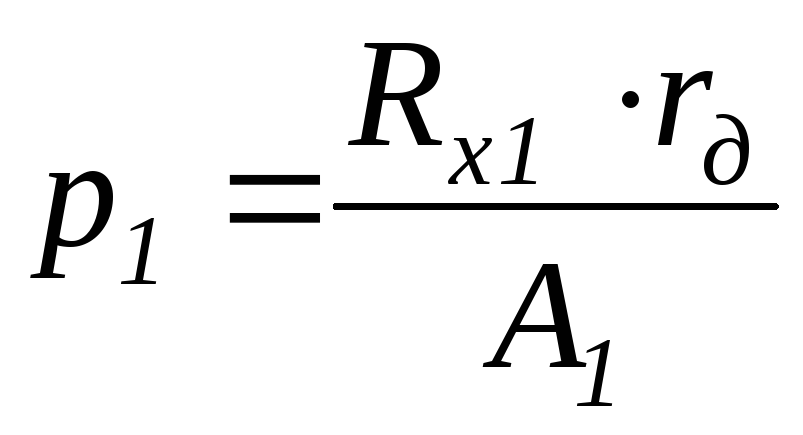 –давление,
необходимое для доведения передних
тормозов до юза.
–давление,
необходимое для доведения передних
тормозов до юза.
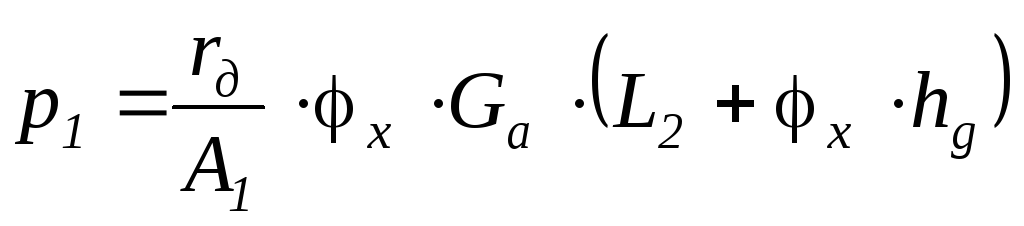 .
.
Аналогично найдем давление в заднем контуре:
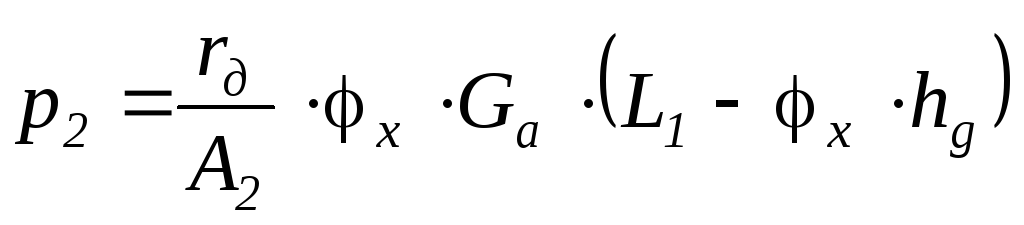 .
.
Соотношение давлений в контурах:
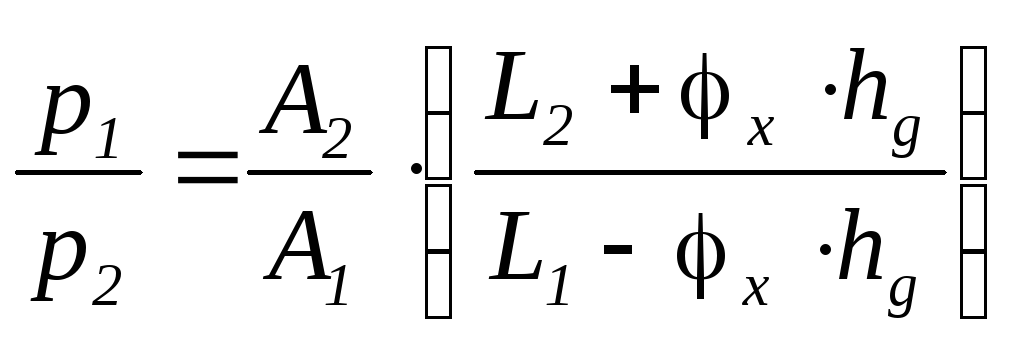
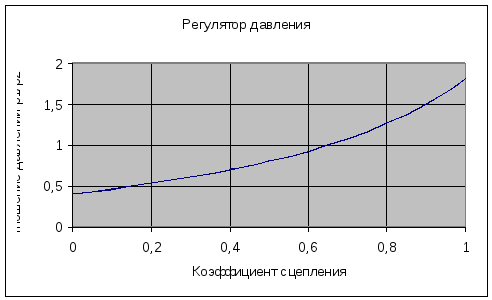 .
.
Ga= | 15600н |
L= | 1,5м |
L1= | 0,825м |
L2= | 0,675м |
hg= | 0,5м |
А2/А1= | 0,5 |
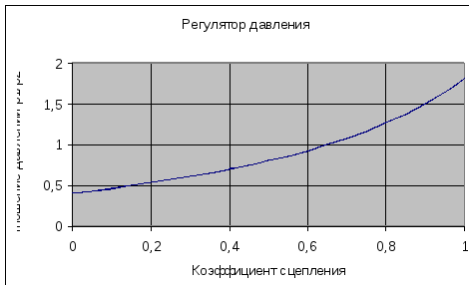
Полученная характеристика является идеальной и показывает необходимое соотношение давлений в исполнительных механизмах передних и задних колес для одновременного доведения колес обоих осей до юза. Если в тормозном приводе не предусмотрено никаких регулирующих давление механизмов и главный тормозной непосредственно связан с рабочими цилиндрами, то давление в исполнительных механизмах передних и задних тормозов всегда будет одинаковым, т.е. будет характеризоваться прямой линией. Таким образом, идеальная и реальная при отсутствии регулирующих механизмов) характеристики совпадают только в одной точке, т.е. для данного автомобиля при заданной развесовке одновременно до юза будут доведены колеса обеих осей только на одной дороге с характерным значением коэффициента сцепления. Н дорогах с меньшим сцеплением раньше в юз попадут колеса передней оси, а на дорогах с большим сцеплением – колеса задней оси.
Колеса, доведенные до юза, не способны воспринимать боковые нагрузки: Любое внешнее воздействие приводит к заносу.
При опережающем юзе передних колес автомобиль движется не управляемо, но устойчиво прямолинейно.
При опережающем юзе задних колес автомобиль попадает в прогрессирующий занос, что означает потерю устойчивости.
Несовпадение идеальной и реальной характеристик распределения давлений в зоне малых коэффициентов сцепления можно считать допустимым, так как в процессе экстренного торможения (а именно в этом случае колеса автомобиля доводятся до полного юза) главная задача – остановить автомобиль на полосе движения, а опережающий юз колес передней оси ведет к устойчивому прямолинейному движению.
Несовпадение идеальной и реальной характеристик распределения давлений в зоне больших коэффициентов сцепления абсолютно недопустимо, так как прогрессирующий занос, возникающий в этом случае, является причиной потери полосы движения в процессе экстренного торможения и приводит к большинству аварий с тяжелыми последствиями при экстренном торможении.
2.4.Силы, действующие на автомобиль при торможении. Уравнение тормозного баланса.
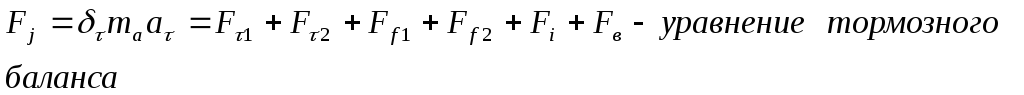

Тормоз. силы
определяются 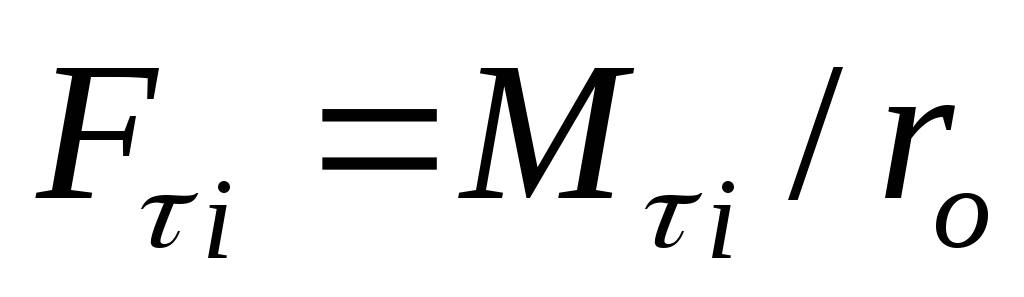
Максимальное значение ограничено по сцеплению с дорогой;
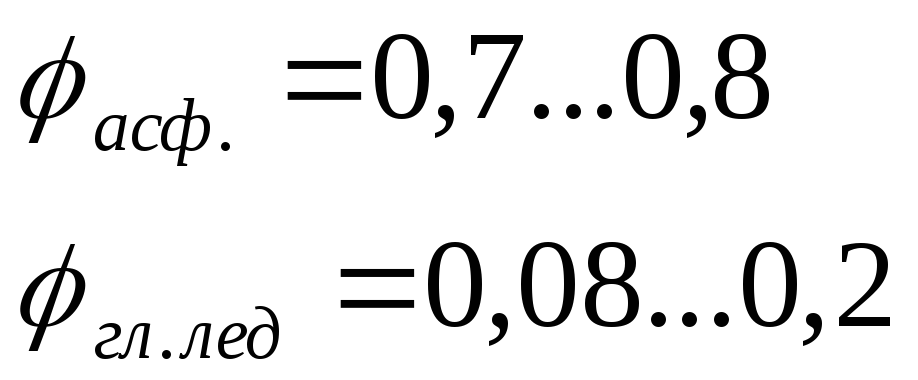
Обозначим 
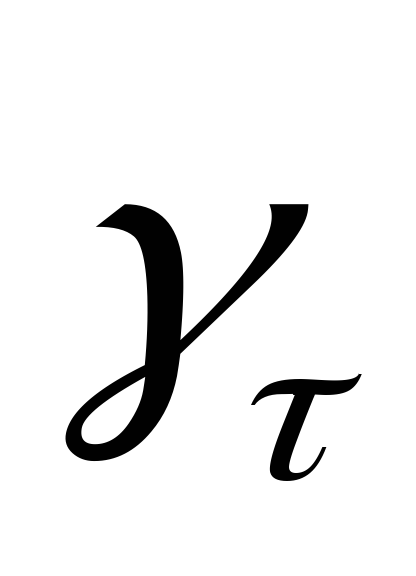 —
удельная тормозная сила.
—
удельная тормозная сила.
 — динамический
(тормозной) фактор.
— динамический
(тормозной) фактор.
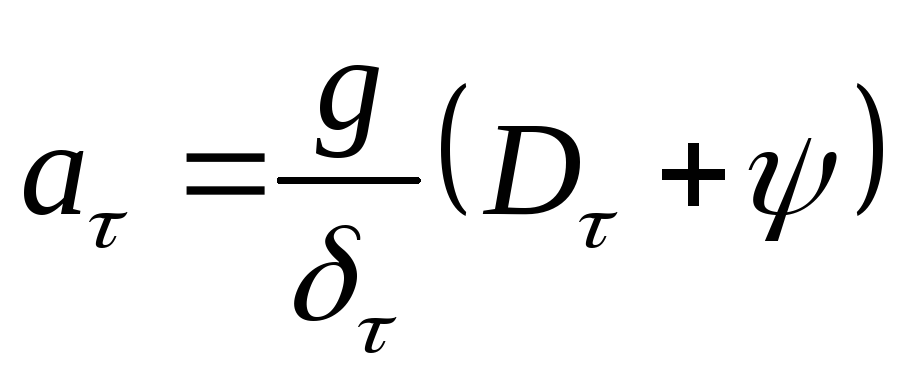
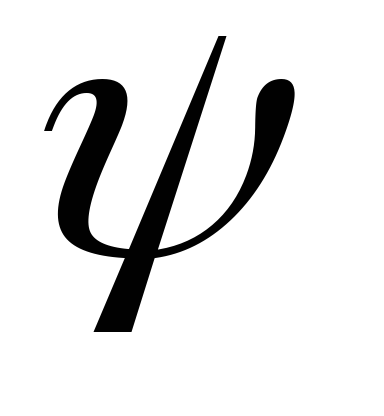 —
коэффициент сопротивления дороги
—
коэффициент сопротивления дороги
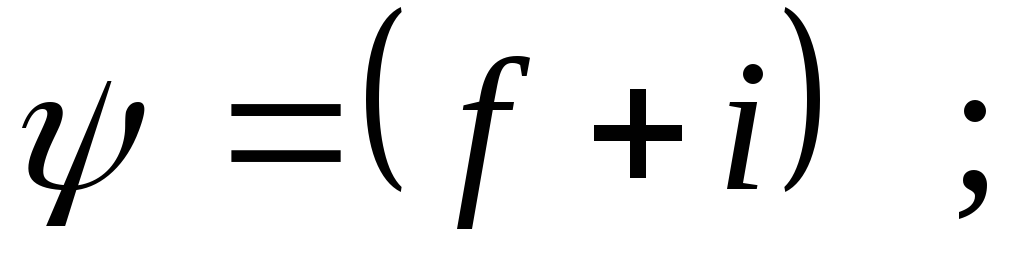
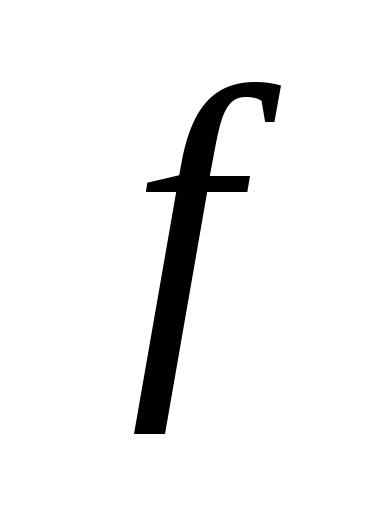 —
коэффициент сопротивления качению
—
коэффициент сопротивления качению
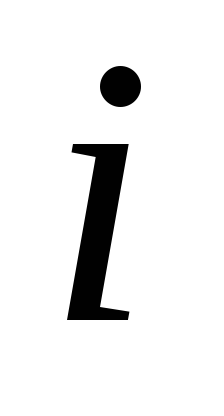 — уклон
— уклон
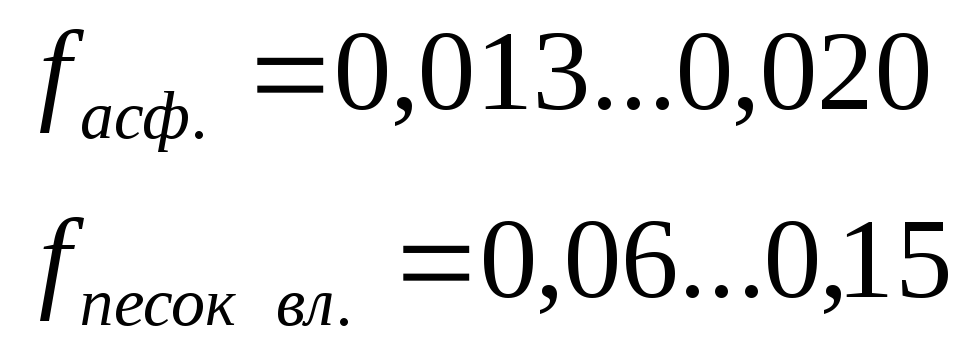
Максимальная тормозная сила достигается при определённом проскальзывании шин в зоне контакта с дорогой. Тормозные системы авто целесообразно конструировать так, чтобы по возможности исключить блокировку колёс.
При полном юзе даже небольшие боковые силы могут вызвать боковое скольжение колес. Особенно опасна блокировка заднего моста раньше передних колёс.
Для того чтобы обеспечить одинаковое скольжение всех колёс, необходимо:
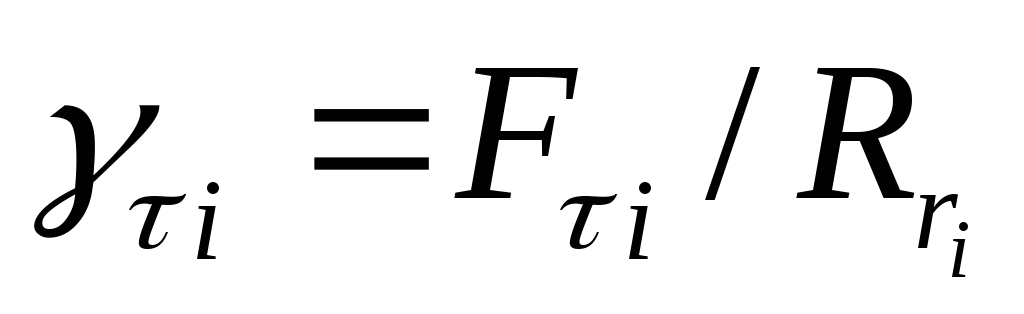 м.б. в знаменателе
сумма?
м.б. в знаменателе
сумма?
т.е. тормозные силы
распределялись пропорционально 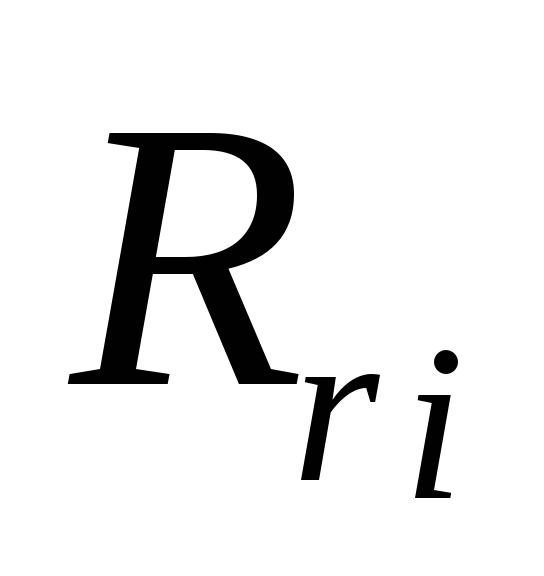 (или пропорционально
нагрузке мостов).
(или пропорционально
нагрузке мостов).
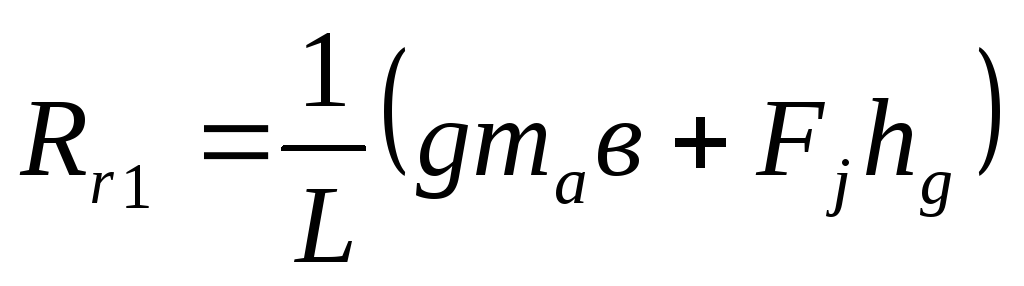
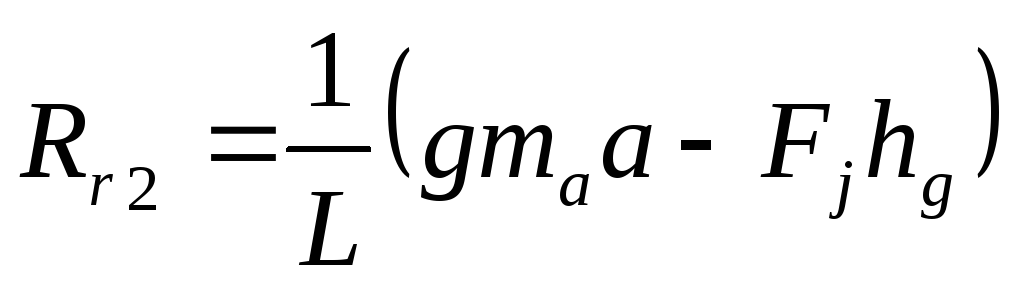
При торможении, 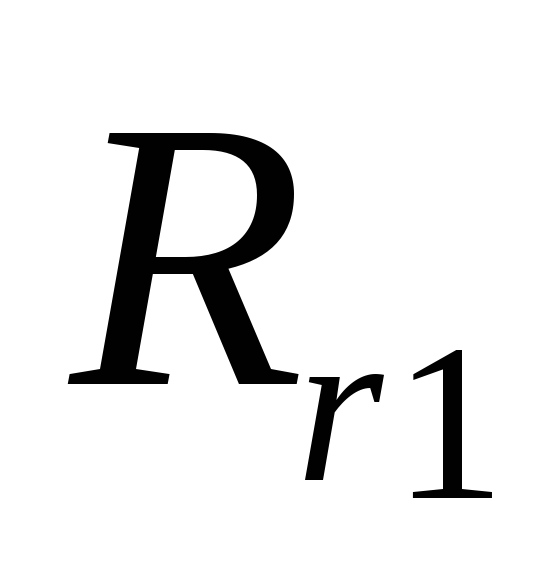 —
увеличивается,
—
увеличивается, 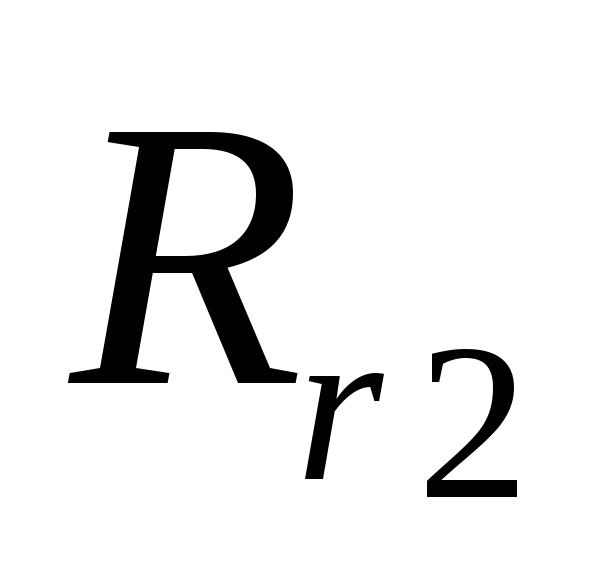 —
уменьшается.
—
уменьшается.
Степень перераспределения зависит от интенсивности торможения
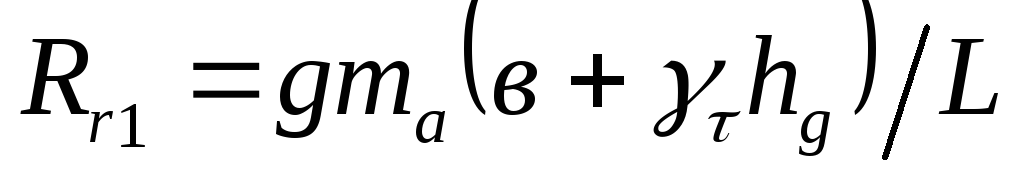
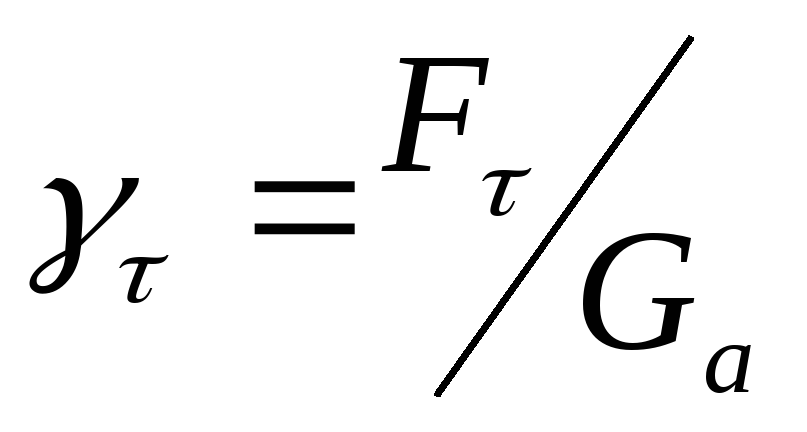
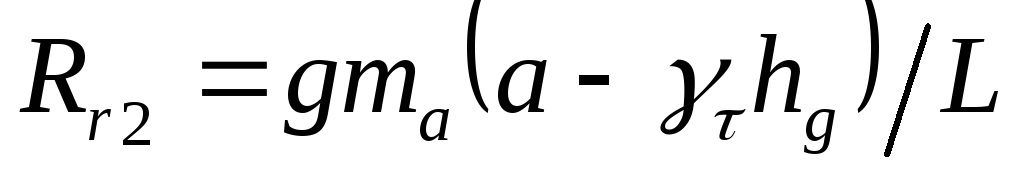
В условиях полного использования сцепления
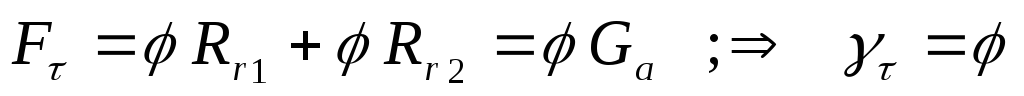
Следовательно,
при этом 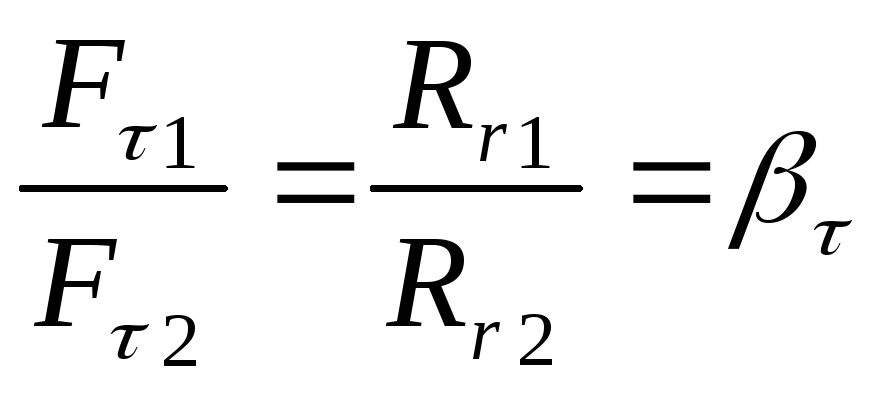 — коэффициент распределения тормозных
сил.
— коэффициент распределения тормозных
сил.
Оптим 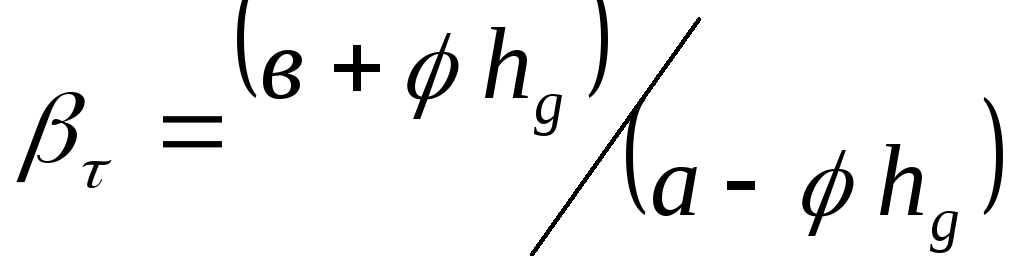 (0,65)
(0,65)
3.Конструкции автомобильных тормозов и тормозных механизмов.
3.1.Классификация
Тормозная система автомобилей (и тракторов) состоит из — тормозного механизма и — тормозного привода.
Тормозной механизм служит для замедления транспортного средства (чаще всего за счет сил трения).
Тормозные механизмы различают: — колесные
— центральные (трансмиссионные)
По типу тормозных деталей: — ленточные
— колодочные
— дисковые
На автомобилях применяются два последних типа.
На всех отечественных автомобилях (грузовых) используются колодочные тормоза барабанного типа в качестве рабочих и стояночных тормозов.
Колодочные тормоза барабанного типа представляют собой пару тормозных колодок, смонтированных внутри тормозного барабана, который вращается вместе со ступицей колеса, колодки раздвигаются кулаками или поршнями гидроцилиндров, прижимаясь таким образом к тормозному барабану.
Регулирование тормозов, величина создаваемого тормозного момента, характер изнашивания тормозных накладок в значительной мере зависят от способа крепления колодок к опорному диску
Дисковые тормоза (ГАЗ-3102, ВАЗ 2101, Москвич-2140 передние колеса и т.д.) обладают более высокой эффективностью.
На ступице укрепляется чугунный тормозной диск. С двух сторон этого диска помещены тормозные накладки, которые при помощи г/ц прижимаются к диску и осуществляется торможение автомобиля
12 Тормозная динамика автомобиля и ее значение для безопасности движения. Требования к тормозным системам.
Во время движения водитель постоянно изменяет скорость автомобиля в соответствии с дорожной обстановкой и должен в любое время быть готовым к экстренной остановке в случае необходимости. Для этого на автомобиле имеются специальные системы, которые создают большое дополнительное сопротивление движению автомобиля и обеспечивают быстрое снижение его скорости вплоть до полной остановки. Эти системы называются тормозными. Современные автомобили оборудуются четырьмя тормозными системами: рабочей, запасной, стояночной и вспомогательной.
Основной тормозной системой является рабочая. Она предназначена для регулирования скорости автомобиля в любых условиях движения. Запасная система используется в случае отказа рабочей, а стояночная удерживает неподвижный автомобиль на месте. Вспомогательная тормозная система служит для поддержания скорости автомобиля постоянной в течение длительного периода времени на спусках без применения рабочей. На легковых автомобилях и на грузовых малой и средней грузоподъемности в качестве запасной тормозной системы используют стояночную, а в качестве вспомогательной — двигатель. Грузовые автомобили большой грузоподъемности и автобусы большой вместимости оснащаются всеми четырьмя отдельными тормозными системами.
Для обеспечения безопасности движения автомобиля рабочая тормозная система должна удовлетворять следующим требованиям:
Время срабатывания системы должно быть минимальным, а замедление автомобиля — максимальным во всех условиях эксплуатации.
Все колеса автомобиля должны затормаживаться одновременно и с одинаковой интенсивностью.
Тормозные силы на колесах должны нарастатЛсгджнож системе не должно быть заеданий и заклиниваний.
Работа тормозной системы не должна вызывать потери устойчивости автомобиля.
Усилия, необходимые для приведения системы в действие и перемещения рабочих органов управления (педали и рычаги), не должны превышать физических возможностей водителя.
Эффективность системы должна быть постоянной в течение всего срока службы автомобиля, а вероятность отказов минимальной.
13 Силы, действующие на автомобиль при торможении.
Рассмотрим силы, действующие на авто при торможении. Приняв допущение, что сопротивление дороги и воздуха отсутствуют а коэф. учета вращения масс равен 1.

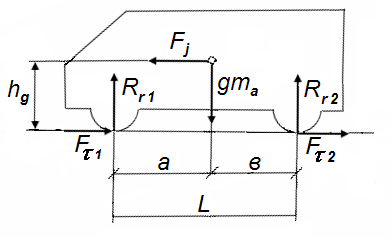
a, b и hц — расстояние от центра тяжести автомобиля соответственно до передней и задней осей и до поверхности дороги, м; L — база автомобиля, м; RxlRX2> Rz1 RZ2 _ соответственно касательные и вертикальные реакции дороги на колесах передней и задней осей, Н; Ри — сила инерции автомобиля, Н.
При принятых допущениях согласно условиям равновесия можно записать:
Fj=Rx1+Rx2
Cост. Уравнение моментов сил относительно точек контактов:
Rz1*L-Fj*hц-G*b=0 -Rz2*L-Fj*hц+G*a=0
Из этих уравнений получим:
Rz1=(G*b+Fj*hц)/L Rz2=(G*a-Fj*hц)/L
Как видно из полученных выражений, при торможении автомобиля вертикальная реакция на передних колесах Rzl растет, а на задних Rz2 –уменьшается.
Предельное значение касательной реакции дорог, обусловленно сцеплением шин с дорогой наз. силой сцепления.
Таким образом, конструкция тормозной системы должна создавать разное соотношение тормозных сил Rxi и Rx2 при торможении с различной интенсивностью. Указанное требование трудно выполнимо и многие автомобили имеют тормозные системы, обеспечивающие постоянное соотношение тормозных сил. У таких автомобилей колеса передней и задней оси блокируются не одновременно. Этот недостаток устраняют путем применения регуляторов давления и антиблокировочных устройств, которые мы рассмотрим позже.
17. Пути повышения тормозной динамики автомобиля
Тормозная система необходима на автомобиле для снижения его скорости, остановки и удерживания на месте.
Тормозная сила возникает между колесом и дорогой по направлению, препятствующему вращению колеса. Максимальное значение тормозной силы на колесе зависит от возможностей механизма, создающего силу торможения, от нагрузки, приходящейся на колесо, и от коэффициента сцепления с дорогой. При равенстве всех условий, определяющих силу торможения, эффективность тормозной системы будет зависеть в первую очередь от особенностей конструкции механизмов, производящих торможение автомобиля.
На современных автомобилях в целях обеспечения безопасности движения устанавливают несколько тормозных систем, выполняющих различное назначение. По этому признаку тормозные системы подразделяют на: рабочую, запасную, стояночную и вспомогательную.
Повышение максимальных и средних скоростей движения, а также увеличение плотности транспортных потоков — основная причина установления жестких требований к эффективности и надежности тормозных систем автомобилей. Для повышения эффективности торможения автомобиля применяют регуляторы, обеспечивающие более полное использование сцепления с дорогой колесами различных осей, устанавливают быстродействующие тормозные приводы, а для увеличения тормозного момента — усилители. Надежность работы тормозной системы значительно повышается при использовании раздельного — двухконтурного привода.
18 Показатели устойчивости автомобиля
Устойчивость автомобиля это совокупность его качеств, обеспечивающих движение в требуемом направлении без бокового скольжения (заноса) или опрокидывания. Устойчивость является одним из важнейших эксплуатационных свойств автомобиля, от которого во многом зависит безопасность движения. Управляя неустойчивым автомобилем, водитель вынужден более внимательно следить за дорожной обстановкой и постоянно корректировать движение автомобиля, чтобы он не выехал за пределы дороги.
В зависимости от направления бокового скольжения или опрокидывания различают поперечную и продольную устойчивость. Более вероятна и опасна потеря поперечной устойчивости, возникающая вследствие действия различных боковых сил.
Потеря поперечной устойчивости может произойти как при криволинейном, так и при прямолинейном движении.
Показателями поперечной устойчивости автомобиля при криволинейном движении являются максимальные (критические) скорости движения по дуге окружности, соответствующие началу заноса V3 и началу опрокидывания Vonp.
Потеря поперечной устойчивости при прямолинейном движении может наступить, если автомобиль движется по косогору, т. е. по дороге с поперечным уклоном. В этом случае показателями поперечной устойчивости являются максимальный (критический) угол косогора, соответствующий началу поперечного скольжения колес.
Опрокидывание автомобиля в продольной плоскости практически не встречается. Потеря автомобилем продольной устойчивости выражается, как правило, в буксовании ведущих колес, особенно часто наблюдаемом при преодолении автопоездом затяжных крутых подъемов со скользкой поверхностью. Показателем продольной устойчивости служит максимальный угол подъема, преодолеваемый автомобилем без буксования ведущих колес.
Свойство автомобиля двигаться прямолинейно без корректирующих действий водитель при неизменном положении рулевого колеса, называется курсовой устойчивостью. Автомобиль с плохой курсовой устойчивостью самопроизвольно меняет направление движения (рыскает по дороге), создавая угрозу другим транспортным средствам и пешеходам.
7. Тормозные свойства
Тормозные свойства имеют важное значение при эксплуатации автомобилей, так как от них во многом зависит безопасность движения. Чем лучше тормозные свойства, тем выше безопасность движения, средняя скорость и производительность автомобиля.
7.1. Измерители тормозных свойств
Измерителями тормозных свойств автомобиля являются замедление при торможении jз, м/с2, время торможения tтор, с, и тормозной путь Sтop, м. Наиболее важное значение из указанных измерителей имеют замедление и тормозной путь.
Нагрузка на автомобиль оказывает существенное влияние на его тормозные свойства. Поэтому в процессе эксплуатации для проверки эффективности тормозных механизмов в качестве измерителей используют максимально допустимый тормозной путь и минимально допустимое замедление автомобиля без нагрузки и с полной нагрузкой.
Нормативные значения измерителей тормозных свойств автомобиля без нагрузки при торможении на сухой асфальтовой горизонтальной дороге регламентированы правилами дорожного движения.
7.2. Уравнение движения при торможении
Уравнение движения автомобиля выведем для случая торможения на горизонтальной дороге (рис. 7.1). Спроецируем все силы, действующие на автомобиль, на плоскость дороги и получим следующее уравнение движения при торможении:
Pи=Rх1– Rх2–Pв=0
Замедление при торможении определим из этого уравнения, представив его в следующем виде:
 ,
,

Рис. 7.1. Силы, действующие на автомобиль при торможении откуда

Значение замедления зависит от режима торможения автомобиля. При эксплуатации применяется экстренное (аварийное) и служебное торможение.
7.3. Экстренное торможение
Экстренным называется режим торможения, при котором тормозные силы на колесах автомобиля достигают максимально возможного значения по сцеплению.
При этом колесо находится на грани юза (полного скольжения), но еще катится с некоторым проскальзыванием. Как показали исследования, максимальное значение тормозной силы на колесе достигается при его 15…30%-ном проскальзывании.
Экстренное торможение применяется сравнительно редко и обычно составляет 3…5% общего числа торможений. При экстренном торможении замедление достигает наибольшего значения и на сухом асфальтобетоне составляет 7,5… 8 м/с2. Экстренное торможение очень неприятно для сидящих пассажиров и опасно для стоящих. Оно вызывает повышенный износ шин и тормозных механизмов. При экстренном торможении для увеличения замедления необходимо уменьшить влияние вращающихся масс, поэтому двигатель отключается от трансмиссии при помощи сцепления. Процесс торможения осуществляется только тормозной системой.
При экстренном торможении скорость автомобиля резко падает, поэтому влияние силы сопротивления воздуха незначительно. Уравнение движения автомобиля при экстренном торможении принимает следующий вид:
Pи – Rх1 – Rх2=0
Так как при экстренном торможении касательные реакции дороги на передних и задних колесах имеют максимально возможные значения по сцеплению, то

Rх1+Rх2=Rz1φx+Rz2φx= =(Rz1+Rz2)φx=Gφx
С учетом этого выражения для горизонтальной дороги и современных автомобильных дорог, имеющих небольшие уклоны, при экстренном торможении замедление
jз=gφx,
где φx — коэффициент сцепления колес с дорогой.
Рис. 7.2. Зависимости замедления Уз, времени торможения tTOp, тормозного STop и остановочного So путей автомобиля от скорости движения v
Если во время торможения значение коэффициента сцепления колес с дорогой не изменяется, то замедление не зависит от скорости в течение всего периода торможения (рис. 7.2).
Устойчивость автомобиля при торможении
На графике должно быть две кривые (в нашем случае одна), соответственно для транспортного средства полной массы и для снаряженного состояния с водителем.
График, представленный на рис.3 построен для реального автомобиля. Его параметры таковы: Мерседес E-220, W210, масса ma = 1700 кг; расстояние от центра масс до передней оси a = 1,33 м; от центра масс до задней оси b = 1,27 м; распределение масс соответствует 48,8:51,2 высота расположения центра масс h = 0,57 м.
Построенный график позволяет провести определенный анализ. Так, точки пересечения линий максимальных тормозных сил, определяемых по формулам (1.6) и (1.7), с координатными осями показывают максимально досягаемую тормозную силу при отказе одного из контуров торможения. Поэтому они называются также точками отказа, соответственно точка B характеризует отказ контура передней, а точка C отказ контура задней оси.
Соединив точки одинаковых значений удельных тормозных сил передней и задней оси, получим линии равных замедлений, выраженных в долях g. Они пересекают линию оптимального распределения в точках пересечения линий предельных значений удельных тормозных сил, соответствующих коэффициенту сцепления ϕx = j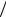 g – точка A.
g – точка A.
Любое отклонение фактического распределения тормозных сил от оптимального приводит к ухудшению тормозных свойств автомобиля.
Равенство тормозных сил правой и левой стороны у тормозящего автомобиля обеспечивается не всегда. Причин этому существует множество. Вот далеко не полный перечень:
неравенство тормозных сил колес правой и левой стороны из-за различных свойств дорожного покрытия под колесами правой и левой стороны автомобиля;
неравенство тормозных сил колес правой и левой стороны автомобиля из-за неисправностей тормозной системы;
боковой ветер, который перераспределяет вес автомобиля;
торможение на дороге с поперечным уклоном.
Определение сил, действующих на автомобиль при его движении и торможении
3 Определение сил, действующих на автомобиль при его движении и торможении
Цель работы:
— Научиться определять величину сил, действующих на автомобиль при его движении.
— Научиться определять величину сил, действующих на автомобиль при его торможении.
— Научится определять основные измерители тормозных качеств автомобиля.
— Научится пользоваться расчетными таблицами.
3.1 Ход работы
3.1.1 Данные для расчета
Определить силы
действующие на автомобиль при его движении и торможении, если вес автомобиля Ga = т; имеет задний
привод и движется со
скоростью км/ч в гору; угол уклона 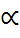 g= ; база автомобиля L = м; максимальная высота
автомобиля Н = м.
g= ; база автомобиля L = м; максимальная высота
автомобиля Н = м.
3.1.2 Расчетная база
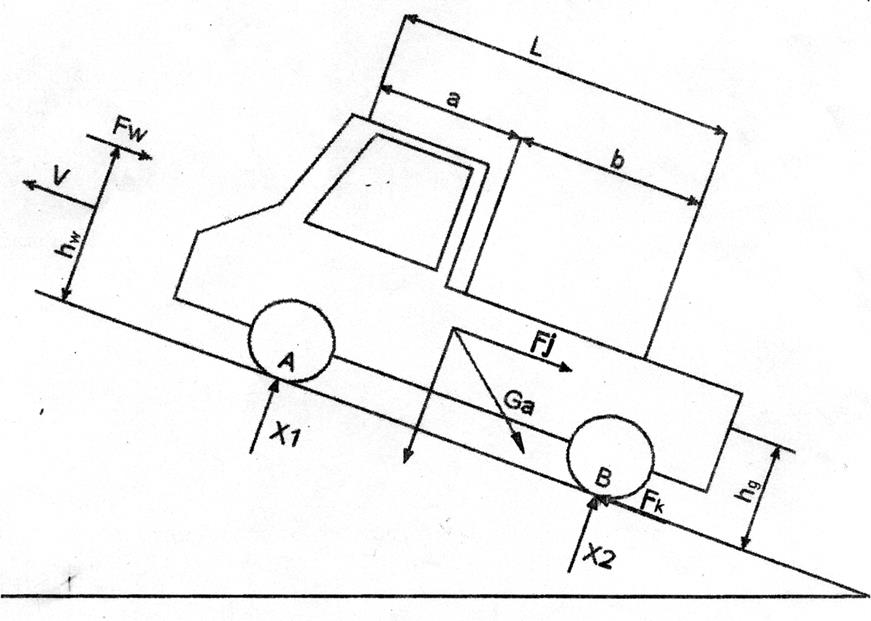
3.1.3 Тяговая сила, действующая на автомобиль.
Fk = G2 · ƒ = Н
где G2 = 1/3 Gа = Н — вес автомобиля, приходящийся на ведущие колёса ƒ = 0,5 … 0,8 — коэффициент сцепления
3.1.4 Сила сопротивления качению.
Ff = Ga· f = H
где f = 0,018 — коэффициент сопротивлению качению
3.1.5 Лобовая площадь автомобиля.
А = В1 · Н = м2
где В1 = м — колея колёс,
Н = м — наибольшая высота автомобиля.
3.1.6 Сила сопротивления воздуха.
Fw = Rw · А · Va2 = Н
где Rw = Нс2 — коэффициент обтекаемости автомобиля,
Va = м/с — скорость автомобиля в м/с
3.1.7 Сила сопротивления подъему
Fh = Ga · jg = Н
где jg = tgag = — уклон дороги
3.1.8 Сила инерции
Равна нулю, т.к. автомобиль движется равномерно.
3.1.9 Нормальная реакция, действующая на задние колёса автомобиля
Х2 = Ga · a cosαg/L – f · ha = H
где cosαg = cos 0 =
f = — коэффициент сцепления с дорогой
ha = м — высота центра массhg
а = 1 / 3 L = м , где L = м — база автомобиля
3.1.10 Нормальная реакция, действующая на передние колёса автомобиля.
Х2 = Ga · a cosαg 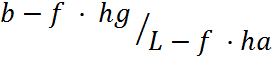 =
H
=
H
3.1.11 Нормальные реакции (в статическом состоянии на горизонтальной плоскости)
X1| = Gab/L = H
X1| = Gaa/L = H
3.1.12 Коэффициенты продольного распределения нагрузки
m1 = x1/ x1| =
m2 = x2/ x2| =
Основные измерители движения автомобиля при разгоне.
3.1.13 Задаёмся коэффициентом суммарного сопротивления Ψ = ; принять динамический фактор D =
3.1.14 Коэффициент учёта влияния вращающихся масс
SBp = 1 + 0,007ik2 =
где ik = 4 — передаточное число коробки передач
3.1.15 Ускорение автомобиля
Ja = 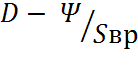 g =
м/с2
g =
м/с2
3.1.16 Время разгона
tp = Vt/1,8 · ja = c
3.1.17 Путь разгона
Sp = Vср · tp/1,8 = м
где Vср = Vt+ V0/2 = м/с – средняя скорость автомобиля при разгоне
Силы и реакции, действующие на автомобиль при его торможении
3.1.18 Максимальная тормозная сила
Fтоp = f · Ga= Н
3.1.19 Нормальная реакция, действующие на передние колёса.
X 1тор = Gaa-Fmophg/L= H
3.1.20 Нормальная реакция, действующие на задние колёса.
X2тор = Gab-Fmophg/L= H
Основные измерители тормозных качеств автомобиля (рассматриваем процесс торможения при максимальном использовании тормозной силы на горизонтальной дороге, пренебрегая сопротивлением воздуха.
3.1.21 Ускорение при торможении
jтор = f · g = м/с2
3.1.21 Путь торможения
Sтор = Va2/254f = м
где Va — 90 км/ч — скорость автомобиля
3.1.23 Время торможения
tтор = Va/f · g = с
3.1.24 Дистанция безопасности
Д.Б. = Sтоp + Sр.в. + Sп =
где Sтоp = м — величина тормозного пути;
Sр.в. = м — путь пройденный автомобилем за время реакции водителя;
Sп = м — путь пройденный автомобилем за время срабатывания привода.
3.2 протокол выполнения работы
Таблица 3.2.1 — Силы, действующие на автомобиль при его движении
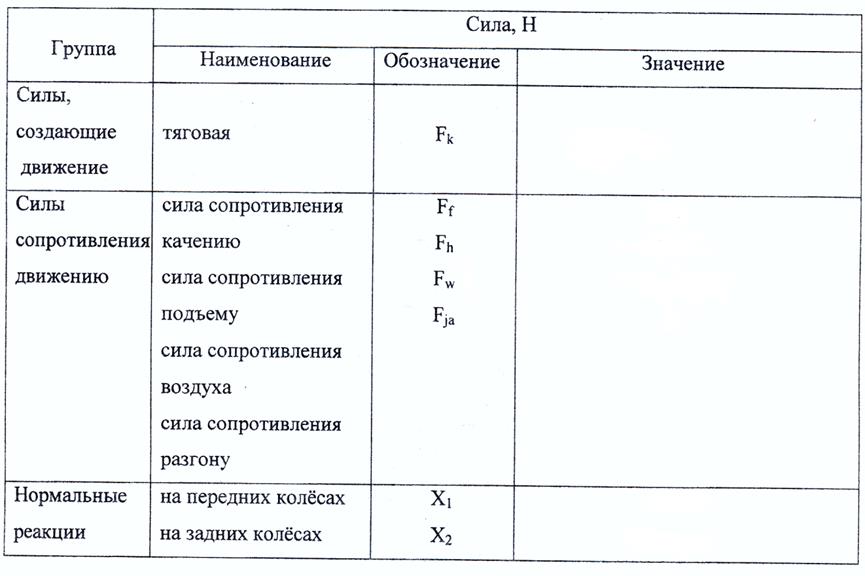
Таблица 3.2.2 – Силы действующие на автомобиль при его торможении

Таблица 3.2.3 – Основные измерительные качества автомобиля

Вывод:
Контрольные вопросы:
— Какие силы действуют на автомобиль при его движении?
— Что такое дистанция безопасности?
— Как определять ускорение, время, путь при его движении автомобиля?
— Как определить суммарный коэффициент сопротивления дороги?
— Как определить динамический фактор автомобиля?
— Как определить нормальные реакции на колесах автомобиля при его движении и торможении?
— Как определить коэффициенты продольного распределения нагрузки?

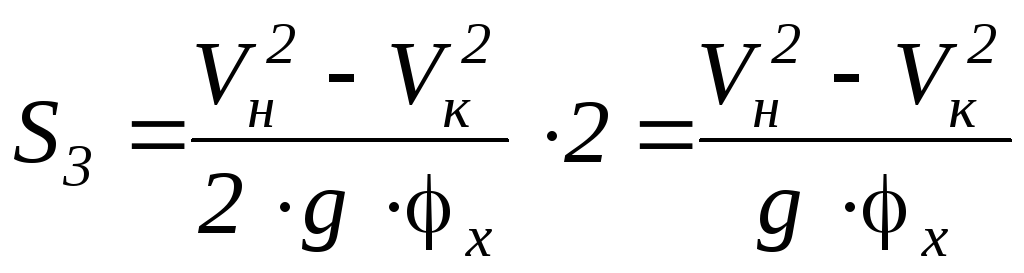 ,
где
,
где