Лямбды что это такое: 403 — Доступ запрещён – Лямбда — Википедия
- 13.06.2020
Лямбда (буква) — это… Что такое Лямбда (буква)?
- Лямбда (буква)
Лямбда (буква)
Λλ
Λ, λ (название: ля́мбда, греч. λάμδα) — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы — ламед. От буквы «лямбда» произошли латинская буква L и кириллическая Л, а также их производные.
Использование
Прописная Λ
Строчная λ
Лямбда в культуре
- В вымышленной вселенной «Звездных Войн» существует космический корабль, известный как «корабль класса Лямбда», похожий на букву «λ», если смотреть вдоль оси симметрии.
- В серии популярных компьютерных игр Half-Life лямбда является логотипом «Комплекса Лямбда», части исследовательского центра Чёрная Меза, в котором изучаются технологии телепортации. Позднее в игре лямбда становится символом сопротивления людей против инопланетного Альянса. Символ также стал символом серии Half-life и часто используется в названии «Half-Life», заменяя букву «a»( H λ L F — L I F E ). Помимо этого, Лямбда заменят букву «А» в названиях модов и различных роликов. Этот символ присутствует и на костюме главного героя — Гордона Фримена.
- В песне Михаила Щербакова «Австралия» лирический герой мечтал дать имя «Лямбда» своему так и не заведённому жирафу, муравьеду или кенгуру.
- Строчная буква лямбда используется в качестве одного из символов ЛГБТ-движения. В 1970 году она была выбрана как символ кампании за легализацию гомосексуальных отношений.
Wikimedia Foundation. 2010.
- Windows Internet Name Service
- Кеторолак
Смотреть что такое «Лямбда (буква)» в других словарях:
буква — Знак (азбучный), письмена (множ. ч.), иероглиф (гиероглиф), каракуля, руны. Нагородил какие то каракули, и читай. .. Ср. знак… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. буква … Словарь синонимов
Буква Л — Буква кириллицы Л Кириллица А Б В Г Ґ Д … Википедия
лямбда — сущ., кол во синонимов: 1 • буква (103) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Лямбда — Греческий алфавит Αα Альфа Νν Ню … Википедия
Лямбда (символ) — Греческий алфавит Α α альфа Β β бета … Википедия
Лямбда-барион — Лямбда барионы (Λ барионы, Λ частицы) группа элементарных частиц, представляющих собой барион с изотопическим спином 0, содержащих ровно два кварка первого поколения (u и d кварк). В состав Λ барионов входит ровно один кварк второго или третьего… … Википедия
Лямбда — (Ламбда, Λ, λ) одиннадцатая буква греческого алфавита; как числовой знак 30. Название от семитического lamed острие (жало) … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
лямбда
Люди (буква) — Буква кириллицы Л Кириллица А Б В Г Ґ Д … Википедия
Альфа (буква) — У этого термина существуют и другие значения, см. Альфа (значения). Греческий алфавит Αα Альфа … Википедия
история и теория / Habr
Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.
Вступление
Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)
Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции,
Термы:
| переменная: | x |
| лямбда-абстракция (анонимная функция): | λx.t, где x — аргумент функции, t — её тело. |
| применение функции (аппликация): | f x, где f — функция, x — подставляемое в неё значение аргумента |
Соглашения о приоритете операций
- Применение функции левоассоциативно. Т.е.
s t u— это тоже самое, что(s t) u - Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е.
λx. λy. x y xозначает то же самое, чтоλx. (λy. ((x y) x)) - Скобки явно указывают группировку действий.
Может показаться, будто нам нужны какие-то специальные механизмы для функций с несколькими аргументами, но на самом деле это не так. Действительно, в мире чистого лямбда-исчисления возвращаемое функцией значение тоже может быть функцией. Следовательно, мы можем применить первоначальную функцию только к одному её аргументу, «заморозив» прочие. В результате получим новую функцию от «хвоста» аргументов, к которой применим предыдущее рассуждение. Такая операция называется
f = λx.λy.t |
Функция с двумя аргументами x и y и телом t |
f v w |
Подставляем в f значения v и w |
(f v) w |
Эта запись аналогична предыдущей, но скобки явно указывают на последовательность подстановки |
((λy.[x → v]t) w) |
Подставили v вместо x. [x → v]t означает «тело t, в котором все вхождения x заменены на v» |
[y → w][x → v]t |
Подставили w вместо y. Преобразование закончено. |
И напоследок несколько слов об области видимости. Переменная
x называется связанной, если она находится в теле t λ-абстракции λx.t. Если же x не связана какой-либо вышележащей абстракцией, то её называют свободной. Например, вхождения x в x y и λy.x yx в λx.x и λz.λx.λy.x(y z) связаны. В (λx.x)x первое вхождение x связано, а второе свободно. Если все переменные в терме связаны, то его называют замкнутым, или комбинатором. Мы с вами будем использовать следующий простейший комбинатор (функцию тождества): id = λx.x. Она не выполняет никаких действий, а просто возвращает без изменений свой аргумент.Процесс вычисления
Рассмотрим следующий терм-применение:
(λx.t) y
Его левая часть — (λx.t) — это функция с одним аргументом x и телом t. Каждый шаг вычисления будет заключаться в замене всех вхождений переменной t на y. Терм-применение такого вида носит имя редекса (от reducible expression, redex — «сокращаемое выражение»), а операция переписывания редекса в соответствии с указанным правилом называется бета-редукцией.
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
(λx.x) ((λx.x) (λz. (λx.x) z)),
который для простоты можно переписать как
id (id (λz. id z))
(напомним, что id — это функция тождества вида λx.x)
В этом терме содержится три редекса:
- Полная β-редукция. В этом случае каждый раз редекс внутри вычисляемого терма выбирается произвольным образом. Т.е. наш пример может быть вычислен от внутреннего редекса к внешнему:
- Нормальный порядок вычислений. Первым всегда сокращается самый левый, самый внешний редекс.
- Вызов по имени. Порядок вычислений в этой стратегии аналогичен предыдущей, но к нему добавляется запрет на проведение сокращений внутри абстракции. Т.е. в нашем примере мы останавливаемся на предпоследнем шаге:
Оптимизированная версия такой стратегии (вызов по необходимости) используется Haskell. Это так называемые «ленивые» вычисления. - Вызов по значению. Здесь сокращение начинается с самого левого (внешнего) редекса, у которого в правой части стоит значение — замкнутый терм, который нельзя вычислить далее.
Для чистого лямбда-исчисления таким термом будет λ-абстракция (функция), а в более богатых исчислениях это могут быть константы, строки, списки и т.п. Данная стратегия используется в большинстве языков программирования, когда сначала вычисляются все аргументы, а затем все вместе подставляются в функцию.
Если в терме больше нет редексов, то говорят, что он вычислен, или находится в нормальной форме. Не каждый терм имеет нормальную форму, например
(λx.xx)(λx.xx) на каждом шаге вычисления будет порождать самоё себя (здесь первая скобка — анонимная функция, вторая — подставляемое в неё на место x значение).Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.
Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y. Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y, а z — первоначальный терм имел бы вид(λx.λz.x)y и после редукции выглядел бы как λz.y. Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.
Так же бывает, что у нас есть абстракция λx.t x, причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t. Такое преобразование называется η-конверсией.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.
Список источников
- «What is Lambda Calculus and should you care?», Erkki Lindpere
- «Types and Programming Languages», Benjamin Pierce
- Вики-конспект «Лямбда-исчисление»
- «Учебник по Haskell», Антон Холомьёв
- Лекции по функциональному программированию
Лямбда-выражение — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2018; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2018; проверки требуют 5 правок.Лямбда-выражение в программировании — специальный синтаксис для определения функциональных объектов, заимствованный из λ-исчисления. Применяется как правило для объявления анонимных функций по месту их использования, и обычно допускает замыкание на лексический контекст, в котором это выражение использовано. Используя лямбда-выражения, можно объявлять функции в любом месте кода.
Лямбда-выражения поддерживаются во многих языках программирования (Common Lisp, Ruby, Perl, Python, PHP, JavaScript (начиная с ES 2015), C#, F#, Visual Basic .NET, C++, Java, Scala, Kotlin, Object Pascal (Delphi), Haxe, Dart[1] и других).
Лямбда-выражения принимают две формы. Форма, которая наиболее прямо заменяет анонимный метод, представляет собой блок кода, заключенный в фигурные скобки. Это — прямая замена анонимных методов. Лямбда-выражения, с другой стороны, предоставляют ещё более сокращенный способ объявлять анонимный метод и не требуют ни кода в фигурных скобках, ни оператора return. Оба типа лямбда-выражений могут быть преобразованы в делегаты.
Во всех лямбда-выражениях используется лямбда-оператор =>, который читается как «переходит в» (в языках Java, F# и PascalABC.NET используется оператор ->). Левая часть лямбда-оператора определяет параметры ввода (если таковые имеются), а правая часть содержит выражение или блок оператора. Лямбда-выражение x => x * 5 читается как «функция x, которая переходит в x, умноженное на 5»[2].
Лямбда — это… Что такое Лямбда?
Λ, λ (название: ля́мбда, греч. λάμδα) — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы 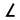 — ламед. От буквы «лямбда» произошли латинская буква L и кириллическая Л, а также их производные.
— ламед. От буквы «лямбда» произошли латинская буква L и кириллическая Л, а также их производные.
Использование
Прописная Λ
Строчная λ
Лямбда в культуре
- В вымышленной вселенной «Звездных Войн» существует космический корабль, известный как «корабль класса Лямбда», похожий на букву «λ», если смотреть вдоль оси симметрии.
- В серии популярных компьютерных игр Half-Life лямбда является логотипом «Комплекса Лямбда», части исследовательского центра Чёрная Меза, в котором изучаются технологии телепортации. Позднее в игре лямбда становится символом сопротивления людей против инопланетного Альянса. Символ также стал символом серии Half-life и часто используется в названии «Half-Life», заменяя букву «a» (H λ L F — L I F E). Помимо этого, Лямбда заменяет букву «А» в названиях модов и различных роликов. Этот символ присутствует и на костюме главного героя — Гордона Фримена. Также напоминает руку, держащую монтировку — известное оружие этой игры.
- В песне Михаила Щербакова «Австралия» лирический герой мечтал дать имя «Лямбда» своему так и не заведённому жирафу, муравьеду или кенгуру.
- В некоторых шрифтах заглавная латинская A рисуется без горизонтальной палочки, т. е. как Λ например, на старом логотипе НАСА или современном логотипе компании Samsung.
- На эмблеме Renault Megane, расположенной на багажнике, в слове Megane используется буква лямбда.
- На эмблеме Kia используется буква лямбда.
Примечания
Где находится лямбда-зонд и что это такое?
В конструкции автомобилей, выпускаемых разными производителями, предусмотрено использование многочисленных датчиков. С их помощью осуществляется непрерывный мониторинг, контроль функционирования различных узлов, систем и агрегатов в заданных параметрах. Важнейшим датчиком является лямбда-зонд (λ-зонд), отвечающий за уровень кислорода в отводимых от двигателя выхлопных газах.
Определение
В соответствии с техническим описанием, лямбда-зонд – это специальное устройство, которое предназначено для фиксации, измерения и оценки уровня содержания (процентного) кислорода в общей массе выхлопных газов ТС. Данная информация в постоянном режиме направляется на электронный блок управления (ЭБУ), где в автоматическом режиме производится корректировка (при необходимости) состава подготавливаемой смеси топлива и кислорода, а также ее качества. В результате обеспечивается снижение уровня токсичности в отработанных газах, выбрасываемых автомобилем в окружающую среду.
Общее устройство
С каждым годом экологические нормы эксплуатации ТС становятся все жестче. Задача снижения уровня токсичности решается конструкторами посредством установки специального элемента – катализатора. Качество, надежность, продолжительность работы каталитического нейтрализатора обеспечивается за счет формирования правильного состава смеси (топливо/ кислород) перед ее направлением в камеру сгорания.
Лямбда-зонд представляет собой специальную систему, которая определяет уровень содержания кислорода, остающегося после завершения процесса превращения энергии сгорания топлива в движущую силу автомобиля. Если датчик зафиксирует излишки свободного кислорода, который не вступит во взаимодействие с топливом, то это указывает на недостаток бензина. С другой стороны, если не хватает кислорода, то следует снизить подачу. Принцип достаточно простой и эффективный, при этом позволяет не только контролировать выхлопные газы, но и обеспечивает экономичный расход топлива.
Месторасположение кислородного датчика
Лямбда-зонд вкручивается непосредственно в систему отвода отработанных выхлопных газов и находится в выпускном тракте в непосредственной близости с катализатором. Последние модели современных автомобилей оснащаются двумя датчиками кислорода, которые устанавливаются по обе стороны от каталитического нейтрализатора. По конструкции оба лямбда-зонда одинаковы, но производят разные замеры.
Так, верхний датчик замеряет и посылает на ЭБУ информацию о том, какой процент кислорода содержится в выхлопных газах. А главная задача кислородного датчика, установленного внизу, заключается в контроле эффективности работы катализатора (при необходимости – в его более тонкой, точечной корректировки).
Общее устройство детали
Наибольшее распространение в современных автомобилях получили кислородные датчики, работающие на основе диоксида циркония. Конструктивно, изделие представляет собой металлический стержень с проводом. Конец стержня несколько скруглен, внутри находится 2 электрода, между которыми – твердый электролит, либо двуокись циркония. Наружный электрод взаимодействует с выхлопными газами, а внутренний – с атмосферой. В конструкции лямбда-зонда предусмотрен специальный термоэлемент, с помощью которого осуществляется быстрый прогрев электродов до требуемых эксплуатационных параметров (приблизительно 300°С).
Возможные неисправности
Кислородные датчики функционируют в крайне тяжелых эксплуатационных условиях при непрерывном и достаточно агрессивном воздействии потока горячих отработанных газов. Выход детали из строя влечет целый ряд характерных неисправностей:
- увеличение расхода топлива;
- неустойчивую работу двигателя на холостом ходу;
- снижение мощности;
- ухудшение тяги, преемственности, передачи крутящего момента на ходовую часть;
- характерный запах бензина из выхлопной трубы.
Поломка датчика редко происходит по причине механического воздействия. Чаще всего это последствия естественного износа, обрыва цепи питания нагревательного элемента или загрязнения.
Заменить неисправный лямбда-зонд можно самостоятельно, но при наличии соответствующей квалификации, либо рекомендуется доверить ремонт специалистам автосервиса.
λ — Греческая строчная буква лямбда (U+03BB) lambda
Описание символа
Лямбда — 11-я буква греческого алфавита (использовалась также в коптском). В ионийской системе счисления соответствовала значению 30. Произошла от финикийской буквы Ламд. От самой лямбды произошли многие буквы, такие как L или Л.
Строчная лямбда широко используется в научной нотации. Лямбдой обозначается длина волны, постоянная распада, удельная теплота плавления, плотность заряда, а также многие другие переменные. λ-зонд — датчик остаточного кислорода в выхлопных газах. λ-фаг — название одного из бактериофагов.
Этот текст также доступен на следующих языках: English;
Похожие символы
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CE BB | 206 187 | 52923 | 11001110 10111011 |
| UTF-16BE | 03 BB | 3 187 | 955 | 00000011 10111011 |
| UTF-16LE | BB 03 | 187 3 | 47875 | 10111011 00000011 |
| UTF-32BE | 00 00 03 BB | 0 0 3 187 | 955 | 00000000 00000000 00000011 10111011 |
| UTF-32LE | BB 03 00 00 | 187 3 0 0 | 3137536000 | 10111011 00000011 00000000 00000000 |
Наборы с этим символом:
Лямбда-исчисление — Википедия
Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем для формализации и анализа понятия вычислимости.
Чистое λ-исчисление, термы которого, называемые также объектами («обами»), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличие каких-либо констант не предполагается.
В основу λ-исчисления положены две фундаментальные операции:
- Абстракция или λ-абстракция (лат. abstractio — отвлечение, отделение) в свою очередь строит функции по заданным выражениям. Именно, если t≡t[x]{\displaystyle t\equiv t[x]} — выражение, свободно[en] содержащее x{\displaystyle x}, тогда запись λx.t[x]{\displaystyle \ \lambda x.t[x]} означает: λ{\displaystyle \lambda } функция от аргумента x{\displaystyle x}, которая имеет вид t[x]{\displaystyle t[x]}, обозначает функцию x↦t[x]{\displaystyle x\mapsto t[x]}. Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы x{\displaystyle x} свободно входило в t{\displaystyle t}, не очень существенно — достаточно предположить, что λx.t≡t{\displaystyle \lambda x.t\equiv t}, если это не так.
Основная форма эквивалентности, определяемая в лямбда-термах, это альфа-эквивалентность. Например, λx.x{\displaystyle \lambda x.x} и λy.y{\displaystyle \lambda y.y}: альфа-эквивалентные лямбда-термы и оба представляют одну и ту же функцию (функцию тождества). Термы x{\displaystyle x} и y{\displaystyle y} не альфа-эквивалентны, так как они не находятся в лямбда-абстракции.
Поскольку выражение λx.2⋅x+1{\displaystyle \lambda x.2\cdot x+1} обозначает функцию, ставящую в соответствие каждому x{\displaystyle x} значение 2⋅x+1{\displaystyle 2\cdot x+1}, то для вычисления выражения
(λx.2⋅x+1) 3{\displaystyle (\lambda x.2\cdot x+1)\ 3},в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм 2⋅x+1{\displaystyle 2\cdot x+1} вместо переменной x{\displaystyle x}. В результате получается 2⋅3+1=7{\displaystyle 2\cdot 3+1=7}. Это соображение в общем виде записывается как
(λx.t) a=t[x:=a],{\displaystyle (\lambda x.t)\ a=t[x:=a],}и носит название β-редукция. Выражение вида (λx.t) a{\displaystyle (\lambda x.t)\ a}, то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ{\displaystyle \lambda }-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ{\displaystyle \lambda }-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.
η{\displaystyle \eta }-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применёнными к любому аргументу, дают одинаковые результаты. η{\displaystyle \eta }-преобразование переводит друг в друга формулы λx.f x{\displaystyle \lambda x.f\ x} и f{\displaystyle f} (только если x{\displaystyle x} не имеет свободных вхождений в f{\displaystyle f}: иначе, свободная переменная x{\displaystyle x} после преобразования станет связанной внешней абстракцией или наоборот).
Функция двух переменных x{\displaystyle x} и y{\displaystyle y} f(x,y)=x+y{\displaystyle f(x,y)=x+y} может быть рассмотрена как функция одной переменной x{\displaystyle x}, возвращающая функцию одной переменной y{\displaystyle y}, то есть как выражение λx.λy.x+y{\displaystyle \ \lambda x.\lambda y.x+y}. Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ{\displaystyle \lambda }-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. Э. Шейнфинкель (1924).
Семантика бестипового λ{\displaystyle \lambda }-исчисления[править | править код]
Тот факт, что термы λ{\displaystyle \lambda }-исчисления действуют как функции, применяемые к термам λ{\displaystyle \lambda }-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ{\displaystyle \lambda }-исчисления. Чтобы придать λ{\displaystyle \lambda }-исчислению какой-либо смысл, необходимо получить множество D{\displaystyle D}, в которое вкладывалось бы его пространство функций D→D{\displaystyle D\to D}. В общем случае такого D{\displaystyle D} не существует по соображениям ограничений на мощности этих двух множеств, D{\displaystyle D} и функций из D{\displaystyle D} в D{\displaystyle D}: второе имеет бо́льшую мощность, чем первое.
Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области D{\displaystyle D} (изначально на полных решётках[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав D→D{\displaystyle D\to D} до непрерывных в этой топологии функций[2]. На основе этих построений была создана денотационная семантика[en] языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.
Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:
- f(n) = 1, if n = 0; else n × f(n — 1).
В лямбда-исчислении, функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого аргумент, ссылающийся на себя (здесь обозначен как r{\displaystyle r}), обязательно должен быть передан в тело функции.
- g := λr. λn.(1, if n = 0; else n × (r r (n-1)))
- f := g g
Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз.
Существует несколько определений комбинаторов неподвижной точки. Самый простой из них:
- Y = λg.(λx.g (x x)) (λx.g (x x))В лямбда-исчислении, Y g{\displaystyle \operatorname {Y\ g} } — неподвижная точка g{\displaystyle \operatorname {g} }; продемонстрируем это:
- Y g
- (λh.(λx.h (x x)) (λx.h (x x))) g
- (λx.g (x x)) (λx.g (x x))
- g ((λx.g (x x)) (λx.g (x x)))
- g (Y g).Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать g (Y g)n{\displaystyle \operatorname {g\ (Y\ g)} n}, где n{\displaystyle n} — число, для которого вычисляется факториал. Пусть n=4{\displaystyle n=4}, получаем:
g (Y g) 4 (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4 (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4 1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0 4·(g(Y g) 3) 4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3) 4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0) 4·(3·(g(Y g) 2)) 4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2)) 4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0)) 4·(3·(2·(g(Y g) 1))) 4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1))) 4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0))) 4·(3·(2·(1·((Y g) 0)))) 4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0)))) 4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0)))) 4·(3·(2·(1·(1)))) 24
Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя Y{\displaystyle \operatorname {Y} }, каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.
В языках программирования под «λ{\displaystyle \lambda }-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции (замыкание).
- ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311—372.
- ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.
- Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.
