Шатунный механизм – Кривошипно-шатунный Механизм Двигателя, Назначение, Принцип Действия и Характеристика КШМ, Диагностика и Ремонт Неисправностей, Конструкция с Чертежами и Схемами

Кривошипно-шатунный механизм — Википедия

Материал из Википедии — свободной энциклопедии

Кривошипно-шатунный механизм (КШМ) предназначен для преобразования возвратно-поступательного движения поршня во вращательное движение (например, во вращательное движение коленчатого вала в двигателях внутреннего сгорания), и наоборот. Детали КШМ делят на две группы, это подвижные и неподвижные детали:

• Подвижные: поршень с поршневыми кольцами, поршневой палец, шатун, коленчатый вал с подшипниками или кривошип, маховик.
• Неподвижные: блок цилиндров (является базовой деталью двигателя внутреннего сгорания) и представляет собой общую отливку с картером, головка цилиндров, картер маховика и сцепления, нижний картер (поддон), гильзы цилиндров, крышки блока, крепежные детали, прокладки крышек блока, кронштейны, полукольца коленчатого вала.

Принцип действия

Прямая схема: Поршень под действием давления газов совершает поступательное движение в сторону коленчатого вала. С помощью кинематических пар «поршень-шатун» и «шатун-вал» поступательное движение поршня преобразуется во вращательное движение коленчатого вала. Коленчатый вал состоит из:

• шатунных шеек
• коренных шеек
• противовеса

Обратная схема: Коленчатый вал под действием приложенного внешнего крутящего момента совершает вращательное движение, которое через кинематическую цепь «вал-шатун-поршень» преобразуется в поступательное движение поршня.

История

В природе

Задние конечности кузнечиков представляют собой кривошипно-шатунный механизм с неполным оборотом.
Бедро и голень человека и роботов-андроидов тоже представляют собой кривошипно-шатунный механизм с неполным оборотом.

В Римской империи

Самые ранние свидетельства появления на машине рукоятки в сочетании с шатуном относятся к пилораме из Иераполиса, 3-й век нашей эры, римский период, а также византийским каменным пилорамам в Герасе, Сирии и Эфесе, Малая Азия (6-й век нашей эры).

[1] Ещё одна такая пилорама возможно существовала во 2 веке н. э. в римском городе Августа-Раурика (современная Швейцария), где был найден металлический кривошип.^[2]

Уравнения движения поршня

Диаграмма показывающая геометрическое положение шатуннопоршневой оси — P, кривошипношатунной оси — N и центра кривошипа — O

Определения

l — длина шатуна (расстояние между шатуннопоршневой осью и кривошипношатунной осью)
r — радиус кривошипа (расстояние между кривошипношатунной осью и центром кривошипа, то есть половина хода поршня

A — угол поворота кривошипа (от «верхней мёртвой точки» до «нижней мёртвой точки»)
x — положение шатуннопоршневой оси (от центра кривошипа вдоль оси цилиндра)
v — скорость шатуннопоршневой оси (от центра кривошипа вдоль оси цилиндра)
a — ускорение шатуннопоршневой оси (от центра кривошипа вдоль оси цилиндра)
ω — угловая скорость кривошипа в радианах в секунду (рад/сек)

Угловая скорость

Угловая скорость кривошипа в оборотах в минуту (RPM):

ω=2π⋅RPM60{\displaystyle \omega ={\frac {2\pi \cdot \mathrm {RPM} }{60}}}

Отношения в треугольнике

Как показано в диаграмме, центр кривошипа, кривошипношатунная ось и шатуннопоршневая ось образуют треугольник NOP.

Из теоремы косинусов следует, что:

l2=r2+x2−2⋅r⋅x⋅cos⁡A{\displaystyle l^{2}=r^{2}+x^{2}-2\cdot r\cdot x\cdot \cos A}

Уравнения по отношению к угловому положению кривошипа (Угловая область)

Уравнения, которые описывают циклическое движение поршня по отношению к углу поворота кривошипа.
Примеры графиков этих уравнений показаны ниже.

Положение

Положение относительно угла кривошипа (преобразованием отношений в треугольнике):

l2−r2=x2−2⋅r⋅x⋅cos⁡A{\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A}

l2−r2=x2−2⋅r⋅x⋅cos⁡A+r2[(cos2⁡A+sin2⁡A)−1]{\displaystyle l^{2}-r^{2}=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}[(\cos ^{2}A+\sin ^{2}A)-1]}

l2−r2+r2−r2sin2⁡A=x2−2⋅r⋅x⋅cos⁡A+r2cos2⁡A{\displaystyle l^{2}-r^{2}+r^{2}-r^{2}\sin ^{2}A=x^{2}-2\cdot r\cdot x\cdot \cos A+r^{2}\cos ^{2}A}

l2−r2sin2⁡A=(x−r⋅cos⁡A)2{\displaystyle l^{2}-r^{2}\sin ^{2}A=(x-r\cdot \cos A)^{2}}

x−r⋅cos⁡A=l2−r2sin2⁡A{\displaystyle x-r\cdot \cos A={\sqrt {l^{2}-r^{2}\sin ^{2}A}}}

x=rcos⁡A+l2−(rsin⁡A)2{\displaystyle x=r\cos A+{\sqrt {l^{2}-(r\sin A)^{2}}}}

Скорость

Скорость по отношению к углу поворота кривошипа (первая производная взята, используя правило дифференцирования сложной функции):

x′=dxdA=−rsin⁡A+(12).(−2).r2sin⁡Acos⁡Al2−r2sin2⁡A=−rsin⁡A−r2sin⁡Acos⁡Al2−r2sin2⁡A{\displaystyle {\begin{array}{lcl}x’&=&{\frac {dx}{dA}}\\&=&-r\sin A+{\frac {({\frac {1}{2}}).(-2).r^{2}\sin A\cos A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}\\&=&-r\sin A-{\frac {r^{2}\sin A\cos A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}\end{array}}}

Ускорение

Ускорение относительно угла кривошипа (вторая производная взята, используя правило дифференцирования сложной функции и частное правило):

x″=d2xdA2=−rcos⁡A−r2cos2⁡Al2−r2sin2⁡A−−r2sin2⁡Al2−r2sin2⁡A−r2sin⁡Acos⁡A.(−12)⋅(−2).r2sin⁡Acos⁡A(l2−r2sin2⁡A)3=−rcos⁡A−r2(cos2⁡A−sin2⁡A)l2−r2sin2⁡A−r4sin2⁡Acos2⁡A(l2−r2sin2⁡A)3{\displaystyle {\begin{array}{lcl}x»&=&{\frac {d^{2}x}{dA^{2}}}\\&=&-r\cos A-{\frac {r^{2}\cos ^{2}A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {-r^{2}\sin ^{2}A}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {r^{2}\sin A\cos A.(-{\frac {1}{2}})\cdot (-2).r^{2}\sin A\cos A}{\left({\sqrt {l^{2}-r^{2}\sin ^{2}A}}\right)^{3}}}\\&=&-r\cos A-{\frac {r^{2}(\cos ^{2}A-\sin ^{2}A)}{\sqrt {l^{2}-r^{2}\sin ^{2}A}}}-{\frac {r^{4}\sin ^{2}A\cos ^{2}A}{\left({\sqrt {l^{2}-r^{2}\sin ^{2}A}}\right)^{3}}}\end{array}}}

Пример графиков движения поршня

График показывает x, x’, x» по отношению к углу поворота кривошипа для различных радиусов кривошипа, где L — длина шатуна (l) и R — радиус кривошипа (r):

Единицами вертикальных осей являются: [дюймы] для положения, [дюймы/рад] для скорости, [дюймы/рад²] для ускорения.
Единицами горизонтальных осей является угол поворота кривошипа в [градусах].

Анимация движения поршня с шатуном одинаковой длины и с кривошипом переменного радиуса на графике выше:

Анимация движения поршня с различными радиусами кривошипа

Применение

Кривошипно-шатунный механизм используется в двигателях внутреннего сгорания, поршневых компрессорах, поршневых насосах, швейных машинах, кривошипных прессах, в приводе задвижек некоторых квартирных и сейфовых дверей. Также кривошипно-шатунный механизм применялся в брусовых косилках.

См. также

Другие способы преобразования вращательного движения в прямолинейное

Здесь была возможность смены Хойкена.

Примечания

1. ↑ ^{1 2} Ritti, Tullia; Grewe, Klaus; Kessener, Paul (2007), «A Relief of a Water-powered Stone Saw Mill on a Sarcophagus at Hierapolis and its Implications», Journal of Roman Archaeology, 20, pp. 138—163
2. ↑ Schiöler, 2009

Литература

• Schiöler, Thorkild (2009), «Die Kurbelwelle von Augst und die römische Steinsägemühle», Helvetia Archaeologica Т. 40 (159/160): 113–124 

Ссылки

Механизм планшайба-стержни — Википедия

Материал из Википедии — свободной энциклопедии

Анимированное изображение планшайбы с валом и стержнями. Вращающийся вал и диск показаны серебристым цветом. Невращающийся диск показан золотистым цветом и шесть стержней приводятся от него в возвратно-поступательное движение. Стержни могут быть присоединены к плунжерам или поршням и вставлены в цилиндры. Мощность может передаваться от вала к плунжерам, как это происходит в аксиально-плунжерном насосе, или от плунжеров мощность может через диск передаваться валу, как это реализовано в аксиально-плунжерном гидромоторе.

Механизм планшайба-стержни (шайбовый механизм) — это механизм, используемый в машиностроении для преобразования движения вращающегося вала в возвратно-поступательное движение стержней параллельно оси вала, или для обратного преобразования.

Данный механизм состоит из вала, двух дисков, называемых планшайбой, и шарнирно прикреплённых к ним стержней. Если диск перпендикулярен валу, то вращение вала будет вызывать вращение одного из дисков, но стержни будут оставаться в покое. Однако малейшее отклонение диска от перпендикулярного положения приведёт к тому, что любая из точек на краю не вращающегося диска будет совершать колебательное движение. Чем больше угол отклонения вращающегося диска от вертикального положения, тем больше амплитуда указанных колебаний. Если к не вращающемуся диску будут прикреплены стержни, то они будут колебаться вместе с краем диска, то есть совершать возвратно-поступательное движение.

Данная конструкция имеет схожие черты с кулачковым механизмом.

Применение механизма планшайба-стержни[править | править код]

Данный механизм может быть использован в двигателях внутреннего сгорания вместо коленчатого вала, как это реализовано в аксиальном двигателе^[1].

Кроме того, этот механизм используется в двигателях Стирлинга.

Как уже упоминалось выше, механизм планшайба-стержни является сердцем аксиально-плунжерных гидромашин (насосов и гидромоторов).

В конструкциях вертолётов важную роль играет автомат перекоса лопастей, который может быть построен на базе механизма планшайба-стержни. В этом случае стержни шарнирно соединены с вращающимся диском, а изменением угла наклона неподвижного диска управляет лётчик из кабины через систему кинематических связей. Этот тип управления углом наклона лопастей используется для создания разной подъёмной силы с разных сторон корпуса вертолёта, что приводит к избирательному наклону машины в разных направлениях.

Описываемый механизм часто используется в некоторых видах расходомеров, применяемых в системах водоснабжения, хотя в них колебательное движение диска не всегда преобразуется в возвратно-поступательное движение.

Активная фазированная антенная решётка выполняется в виде плоского диска, способного сканировать воздушное пространство на угол до 60 градусов в любом направлении от оси самолёта. При закреплении таких радаров на планшайбе угол наклона планшайбы добавляется к углу электронного сканирования. Обычно угол наклона планшайбы выбирается около 40 градусов, и тогда общий угол сканирования радаров достигает 200 градусов^[2].

Другие способы преобразования вращательного движения в прямолинейное:

• Анимационный видеофайл о механизме планшайба-стержни: [1]

• Анимационный видеофайл: [2]

Механизм Чебышёва — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 декабря 2018; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 декабря 2018; проверки требуют 3 правки.

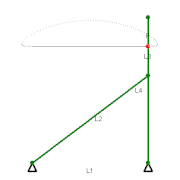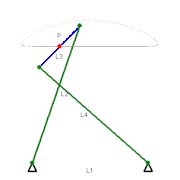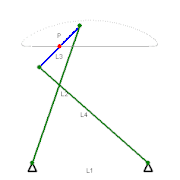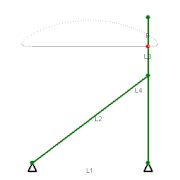
Механизм Чебышёва — механизм, преобразующий вращательное движение в движение, приближённое к прямолинейному.

Механизм Чебышёва был изобретён в XIX веке русским математиком Пафнутием Чебышёвым, проводившим исследования теоретических проблем кинематических механизмов. Одной из таких проблем была проблема преобразования вращательного движения в приближённое к прямолинейному движению.

Прямолинейное движение определяется движением точки P — средней точки звена L₃, расположенной посередине между двумя крайними точками сцепки данного четырёхзвенного механизма. (L₁, L₂, L₃, и L₄ показаны на иллюстрации). При движении по участку, показанному на иллюстрации, точка Р отклоняется от идеального прямолинейного движения. Соотношения между длинами звеньев таковы:

L1:L2:L3=2:2.5:1=4:5:2.{\displaystyle L_{1}:L_{2}:L_{3}=2:2.5:1=4:5:2.}

Точка P лежит на середине звена 

L₃. Приведённые соотношения показывают, что звено L₃ расположено вертикально, когда оно находится в крайних положениях своего движения.^[1]

Длины связаны математически следующим образом:

L4=L3+L22−L12.{\displaystyle L_{4}=L_{3}+{\sqrt {L_{2}^{2}-L_{1}^{2}}}.}

Стопоход П. Л. Чебышёва

На основании описанного механизма Чебышёв изготовил первый в мире шагающий механизм, который пользовался большим успехом на Всемирной выставке в Париже в 1878 году^[2]. Стопоход П. Л. Чебышёва представляет собой четыре объединённых в две пары лямбда механизмов Чебышёва, смонтированных на одном общем основании.

Другими способами преобразования вращательного движения в приближённо прямолинейное являются следующие:

Механизм Кланна — Википедия

Материал из Википедии — свободной энциклопедии

Механизм Кланна (англ. Klann linkage) — это плоский механизм, имитирующий походку животных и способный служить в качестве замены колесу.

Механизм состоит из вращающегося звена, кривошипа, двух шатунов и двух сцепок. Все звенья соединены плоскими шарнирами.

Пропорции каждого из звеньев механизма определяются необходимостью приблизить к линейному характер движения «ножки». За первые пол-оборота кривошипа «ножка» перемещается приближённо линейно, а за оставшиеся пол-оборота она поднимается на заданную высоту, прежде чем вернуться в исходное положение, и цикл начнётся снова. Два таких механизма, соединённые вместе через кривошипы, и сдвинутые друг относительно друга по фазе на пол-цикла, позволяют корпусу машины перемещаться параллельно земле.

Механизм Кланна имеет множество преимуществ шагающего механизма, и лишён, в то же время, некоторых свойственных им ограничений. Он может перешагивать через бордюры, взбираться по ступеням, которые недоступны для колёсных движителей, и в то же время этот механизм не требует управления его двигателями со стороны микропроцессоров, причём количество этих двигателей может быть уменьшено по сравнению с другими видами техники, предназначенной для выполнения тех же функций.

По своей классификации этот механизм находится между шагающими устройствами и колёсными машинами с управляемыми осями.

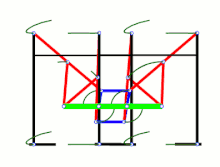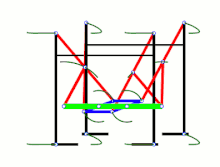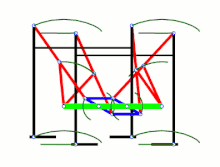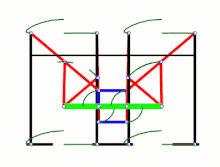
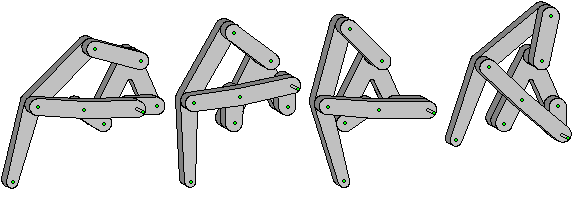Этот рисунок показывает отдельный механизм в разных положениях: полностью вытянутая «ножка», середина шага, полностью втянутая «ножка» и поднятая «ножка». Кривошип (на самом первом рисунке слева он является крайним правым звеном) находится в четырёх положениях: 0, 90, 180 и 270 градусов 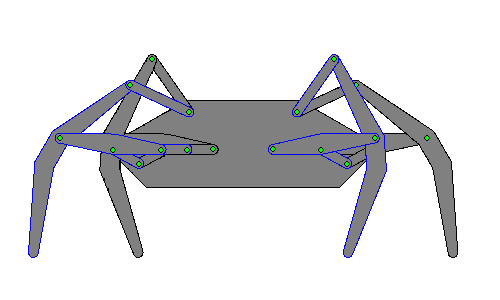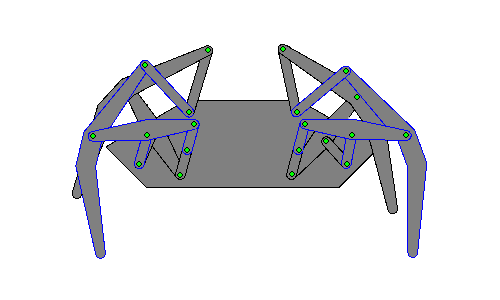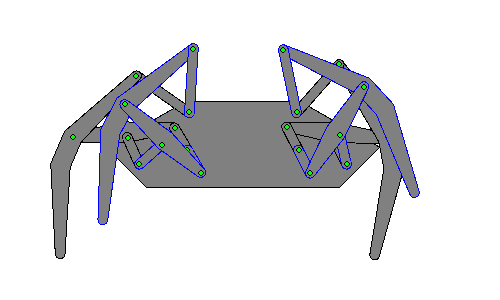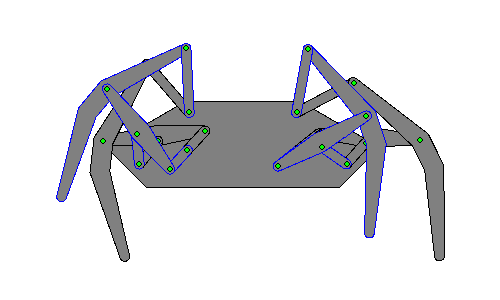Анимированное изображение движения «ног». Ближайшие к зрителю «ноги» очерчены голубым 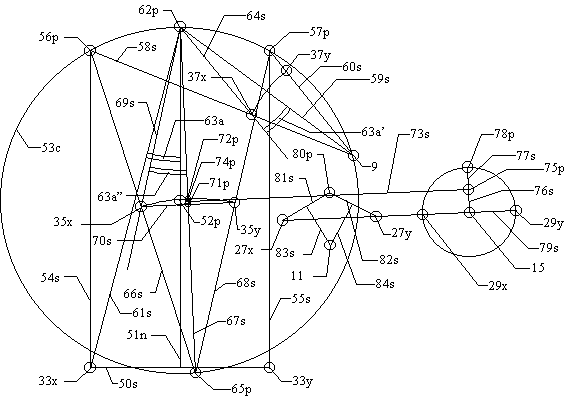Процесс геометрического определения положений каждой из ног, требует анализа 6 переменных, как это описано^[1] в указанных ниже патентах США

Механизм Кланна является не первым шагающим механизмом. Первый в мире шагающий механизм изготовил Пафнутий Чебышёв на основе своего механизма, преобразующего вращательное движение в прямолинейное. Этот шагающий механизм Чебышёва пользовался большим успехом на Всемирной выставке в Париже в 1878 году^[2].

Механизм Кланна был разработан Джо Кланном (Joe Klann) в 1994 году как приложение к теории Бёрместера, используемой при расчётах двухшатунных четырёхзвенных механизмов. Он классифицируется как кинематическая цепь Стефенсона III типа.

• U.S. Provisional Application Ser. No. 60/074,425, was filed on Feb. 11, 1998
• US Patent 6,260,862 ^[3], issued July 17, 2001
• US Patent 6,364,040 ^[4], issued April 2, 2002
• US Patent 6,478,314 ^[5], issued November 12, 2002