Структура машины: Машина — Википедия – Устройство и конструкция автомобиля — Энциклопедия журнала «За рулем»
- 01.04.2020
1.1.2. Структура машин
механизмов регулирования, контроля, управления, защиты, блокировки и др.
Питающее устройство предназначено для непрерывной или периодической подачи объектов (сырья) в машину. Часто такая подача осуществляется путем отмеривания заданных порций продукта (по объему
иреже по массе).
Всоставе привода у машин имеются электродвигатель, как правило, редуктор, передачи гибкой связи, зубчатые и цепные передачи. Заканчивается привод рабочими или распределительно-управляющими валами. На рабочем валу закрепляют рабочий орган, на распределительноуправляющем — ведущие звенья исполнительных механизмов. Распределительно-управляющий вал может служить одновременно и промежуточным, и рабочим валом. Механизмы привода и приводных устройств (трансмиссионные) служат для передачи движения от двигателя к ведущим звеньям исполнительных механизмов или непосредственно к рабочим органам машины.
Исполнительные механизмы служат для преобразования движения (иногда энергии) ведущего звена и передачи его в преобразованном виде ведомому звену (рабочему органу). Исполнительные механизмы, как правило, являются механизмами циклического действия.
Рабочие органы машин бывают основными (обрабатывающими) и вспомогательными (например, удерживающими объект). Они также бывают различными у машин периодического и непрерывного действия. Отличаются они и функциональным назначением. Движение рабочих органов осуществляется по определенным законам и в определенное заданное время.
Механизмы регулирования, контроля, управления, защиты, блокировки и другие обычно состоят из исполнительного механизма циклического действия со вспомогательным рабочим органом. Ведущие звенья этих механизмов также могут закрепляться на распределительноуправляющих валах машины.
Создание машины начинается с представления ее структуры. Анализ условий работы машины немыслим без знания ее структуры. Структуру любой машины представляют в виде структурной схемы. На основании структурной схемы определяют основные размеры машины, осуществляют первое компоновочное решение и набрасывают предварительную кинематическую схему. Структурные схемы машин составляют в соответствии с рекомендуемыми условными обозначениями элементов машин. Нанесение и соединение (линиями или стрелками) условных обозначений для получения структурной схемы начинают от двигателя в последовательности присоединения передач, валов рабочих органов и механизмов. На структурной схеме указывают мощность
Теория механизмов и машин — Википедия
У этого термина существуют и другие значения, см. ТММ.Теория механизмов и машин (ТММ) — это научная дисциплина об общих методах исследования, построения, кинематики и динамики механизмов и машин и о научных основах их проектирования.
В качестве самостоятельной научной дисциплины ТММ, как и многие другие прикладные разделы механики, возникла на волне промышленной революции, начало которой относится к 30-м годам XVIII столетия, хотя машины создавались задолго до этого, и простые механизмы (колесо, винтовая передача и др.) широко использовались ещё во времена Древнего Египта.
Глубокий научный подход в теории механизмов и машин начал широко применяться с начала XIX века. Весь предшествующий период развития техники можно рассматривать как период эмпирического создания машин, на протяжении которого делались изобретения большого количества простых машин и механизмов, среди которых:
 Чебышев П.Л. 1821-1894
Чебышев П.Л. 1821-1894 
Теория механизмов и машин в своём развитии опиралась на важнейшие физические законы — закон сохранения энергии, законы Амонтона и Кулона для определения сил трения, золотое правило механики и др. В ТММ широко используются законы, теоремы и методы теоретической механики. Важное значение для данной дисциплины имеют: понятие передаточного отношения, основы теории эвольвентного зацепления и др.
Можно отметить роль, которую сыграли в создании предпосылок для развития ТММ следующие учёные: Архимед, Дж. Кардано, Леонардо да Винчи, Л. Эйлер, Д. Ватт, Г. Амонтон, Ш. Кулон.
 Франц Рёло́ 1828-1905
Франц Рёло́ 1828-1905Одним из основоположников теории механизмов и машин считается Пафнутий Чебышёв (1812-1894), который во второй половине XIX века опубликовал серию важнейших работ, посвящённых анализу и синтезу механизмов. Одно из его изобретений — механизм Чебышёва.
 Артоболевский И.И. 1905-1977
Артоболевский И.И. 1905-1977В XIX веке развиваются такие разделы, как кинематическая геометрия механизмов (Савари, Шаль, Оливье), кинетостатика (Г. Кориолис), классификация механизмов по функции преобразования движения (Г. Монж), решается задача расчёта маховика (Ж. В. Понселе) и др. Были написаны первые научные монографии по механике машин (Р. Виллис, А. Бориньи), читаются первые курсы лекций по ТММ, выходят первые учебники (А. Бетанкур, Д. С. Чижов, Ю. Вейсбах).
Во второй половине XIX столетия публикуются работы немецкого учёного Ф. Рёло, в которых вводятся важные понятия кинематической пары, кинематической цепи и кинематической схемы.
В советское время крупнейший вклад в становление теории механизмов и машин как отдельной дисциплины внес Артоболевский И.И. Им опубликован целый ряд фундаментальных и обобщающих работ.
В 1969 году он был инициатором создания Международной федерации по теории машин и механизмов (МФТоММ), насчитывающей 45 стран-участниц, несколько раз избирался её президентом.
Машина — технический объект, состоящий из взаимосвязанных функциональных частей (узлов, устройств, механизмов и др.), предназначенный для получения или преобразования механической энергии с целью выполнения возложенных на него функций.
Механизм — система взаимосвязанных тел, предназначенных для преобразования движения одного или нескольких тел в требуемое движение других тел. Механизм составляет основу большинства машин.
Твёрдое тело, входящее в состав механизма, называется звеном. Звено — отдельная деталь, либо группа деталей, жёстко связанных между собой. Звено может состоять из одной или нескольких неподвижно соединённых деталей.
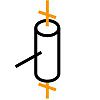
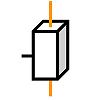
Соединение звеньев, допускающее их относительное движение, называется кинематической парой. Наиболее распространённые кинематические пары: цилиндрический шарнир; шаровой шарнир; ползун и направляющая; винтовая передача. На рисунках приведены условные трёхмерные обозначения типовых кинематических пар для построения пространственных кинематических схем механизмов согласно ISO 3952
-

Цилиндрический шарнир
-

Ползун и направляющая
-

Винтовая пара
-

Сферический шарнир
При построении механизма звенья соединяются в кинематические цепи. Другими словами, механизм – это кинематическая цепь, в состав которой входит неподвижное звено (стойка или корпус (основание)), число степеней свободы которого равняется числу обобщённых координат, характеризующих положения звеньев относительно стойки. Движение звеньев рассматривается по отношению к неподвижному звену – стойке (корпусу, основанию).
Теория механизмов и машин решает следующие задачи:
- анализ механизмов, то есть описание движения, кинематический и динамический анализ существующих и разрабатываемых механизмов;
- синтез механизмов, то есть проектирование структуры и геометрии механизмов на основе заданных кинематических и динамических характеристик;
- задачи теории машин-автоматов, рассматривающей вопросы построения схем автоматических машин, исходя из условий согласованной работы отдельных механизмов, и достижения оптимальной продуктивности, точности и надёжности машин-автоматов.
- Структура механизмов и машин.
- Геометрия механизмов и их элементов.
- Динамика машин и механизмов.
Широкое развитие систем автоматизированного проектирования на базе компьютерной техники позволило существенно снизить трудоемкость ранее применявшихся графических методов анализа и синтеза механизмов. Появилась возможность пространственной анимации виртуальных моделей механизмов. САПР позволяют также проводить проверку на пространственную совместимость звеньев в сложных механизмах, что было весьма затруднительно ранее без изготовления моделей.
Рост вычислительных мощностей позволил отказаться от ранее применявшихся вынужденных упрощений в методиках расчетов.
Широкое распространение получила параметризация моделей, когда, например, геометрические размеры звеньев могут быть изменены на любом этапе проектирования с пересчетом результатов.
- ↑ ISO 3952 Kinematic diagrams — Graphical symbols
Структура машины и ее функциональные части
Билет №1. Структура машины и ее функциональные части. Основные модели ТММ (звено, кинематическая пара, кинематическая цепь) и их свойства.
В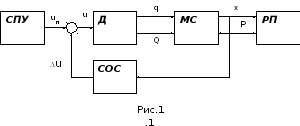 машине можно выделить несколько основных
функциональных частей (рис.1.1). Основную
часть машины составляет исполнительный
механизм, который совершает тот рабочий
процесс, ради которого создавалась
машина. Вместе со вспомогательными
механизмами (например, редуктором,
мультипликатором, коробкой скоростей
и т.п.) он составляет механическую
систему машины (МС). Входу (входному
звену) сообщается движение, определяемое
некоторой обобщенной координатой q.
Механическая система преобразует это
движение в требуемое движение выходного
(рабочего) звена, определяемое выходной
координатой х. К входному звену
приложена обобщенная движущая сила Q,
которая преобразуется в МС в силу Р на выходном звене. Различные расчетные
модели именно этой части машины мы будем
исследовать при рассмотрении вопросов,
связанных со структурой, геометрией,
кинематикой механизмов. При решении
первой задачи динамики оказывается,
что необходимо включить в рассматриваемую
модель и рабочий процесс (РП), который
также можно считать частью машины. МС
совершает рабочий процесс с помощью
силы P, действующей на выходном
звене.
машине можно выделить несколько основных
функциональных частей (рис.1.1). Основную
часть машины составляет исполнительный
механизм, который совершает тот рабочий
процесс, ради которого создавалась
машина. Вместе со вспомогательными
механизмами (например, редуктором,
мультипликатором, коробкой скоростей
и т.п.) он составляет механическую
систему машины (МС). Входу (входному
звену) сообщается движение, определяемое
некоторой обобщенной координатой q.
Механическая система преобразует это
движение в требуемое движение выходного
(рабочего) звена, определяемое выходной
координатой х. К входному звену
приложена обобщенная движущая сила Q,
которая преобразуется в МС в силу Р на выходном звене. Различные расчетные
модели именно этой части машины мы будем
исследовать при рассмотрении вопросов,
связанных со структурой, геометрией,
кинематикой механизмов. При решении
первой задачи динамики оказывается,
что необходимо включить в рассматриваемую
модель и рабочий процесс (РП), который
также можно считать частью машины. МС
совершает рабочий процесс с помощью
силы P, действующей на выходном
звене.
Неотъемлемой частью машины является двигатель (Д), который сообщает механической системе МС движение и в котором создается обобщенная движущая сила Q. Модель двигателя включается в рассмотрение при решении второй задачи динамики – определении закона движения при заданных силах.
Современные машины снабжаются системами программного управления (СПУ), которые формируют управляющие сигналы uп, поступающие на вход двигателя. Для корректировки движения используется система обратной связи (СОС). Она получает информацию о движении выходного звена МС и формирует корректирующий сигнал u, уменьшающий возникающую ошибку.
1.2. Основные модели теории механизмов и машин
Простейшая модель, которой будем пользоваться в дальнейшем – звено. В зависимости от решаемых задач эта модель может обладать разными свойствами (жесткое звено, упругое звено). На первых этапах мы будем считать звено недеформируемым и рассматривать его как абсолютно твердое тело (жесткое звено). Эта модель используется для расчета поведения одной или нескольких жестко связанных между собой деталей. В зависимости от вида движения звенья имеют традиционные названия. Неподвижное звено называется стойкой; на схемах его подчеркивают косой штриховкой. Звено, совершающее вращение вокруг неподвижной оси, называется кривошипом. Если звено совершает качательное движение (неполный оборот), то его называют коромыслом. Звено, совершающее возвратно-поступательное движение, ползун. Звено, совершающее плоское движение шатун. Если звено движется поступательно относительно подвижного звена, то такое звено называют кулисой.
Модель подвижного соединения двух звеньев называется кинематической парой (КП). Эта модель обладает следующими свойствами: элементы кинематических пар считаются недеформируемыми, а связи, накладываемые кинематической парой, являются голономными, стационарными и удерживающими.
Соединив некоторое число звеньев между собой с помощью КП, получим модель, обладающую новыми свойствами – кинематическую цепь. Кинематическая цепь – совокупность звеньев, связанных между собой кинематическими парами (рис.1.10). Она характеризуется числом степеней подвижности или, иначе говоря, числом двигателей, которые надо подсоединить к цепи для того, чтобы полностью определить положение всех звеньев цепи.
 Билет
№2.Основные модели ТММ (механизм,
нормальный механизм, структурная группа,
группа Ассура) и их свойства. Число
степеней свободы и число степеней
подвижности. Формула Малышева.
Билет
№2.Основные модели ТММ (механизм,
нормальный механизм, структурная группа,
группа Ассура) и их свойства. Число
степеней свободы и число степеней
подвижности. Формула Малышева.
Важной характеристикой КП является число степеней свободы s, которое оставляет КП в относительном движении соединяемых ею звеньев. Очевидно, что s + k = 6, где k – число связей, накладываемых КП. Например, если КП оставляет одну степень свободы в относительном движении (s = 1, k = 5), то такую пару называют одноподвижной.
Самое большое число степеней свободы в относительном движении, которое может оставить одна КП, равно пяти, так как КП должна накладывать хотя бы одну связь.
Кинематическая цепь, в которой одно из звеньев принято за неподвижное, называется механизмом. Поскольку неподвижное звено не обладает подвижностью, для определения числа степеней подвижности механизма W это звено нужно вычесть из числа N:
 .
(1.2)
.
(1.2)
Формула
(1.2) называется формулой Малышева–Сомова.
Пользуясь формулой (1.2), определим число
степеней подвижности исполнительного
механизма промышленного робота,
показанного на рис.1.11. Отметим, что все
КП в этом механизме – одноподвижные
(одна поступательная и две вращательных),
тогда: W=6(4 – 1) – 53= = 3.
W=6(4 – 1) – 53= = 3.
Следовательно,
для того, чтобы полностью и однозначно
определить положение звена 4,
необходимо задать 3 входные координаты; на рис.1.11 они
обозначены q1, q2, q3.
Если это условие будет выполнено, то
такой механизм –
нормальный. Нормальным механизмом
называется такой, в котором число входов
совпадает с числом степеней подвижности.
Модель «нормальный механизм» была
предложена проф. М.З.Коловским; она
удобна тем, что поддается геометрическому
анализу. У рассмотренного механизма
(рис.1.11) имеется еще одно важное свойство
– каждое звено соединено с предыдущим
одной КП. В этом случае говорят, что
механизм имеет структуру «дерева».
В этом случае 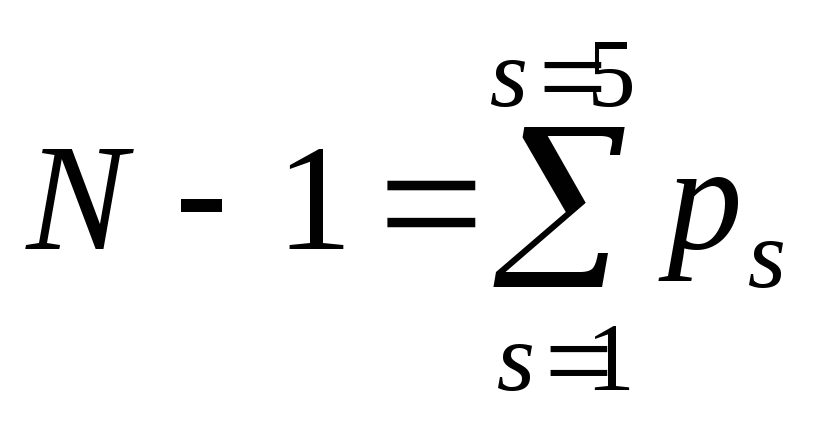 .
.
Формула
Малышева–Сомова (1.2) для механизма со
структурой «дерева» приобретает
следующий вид: 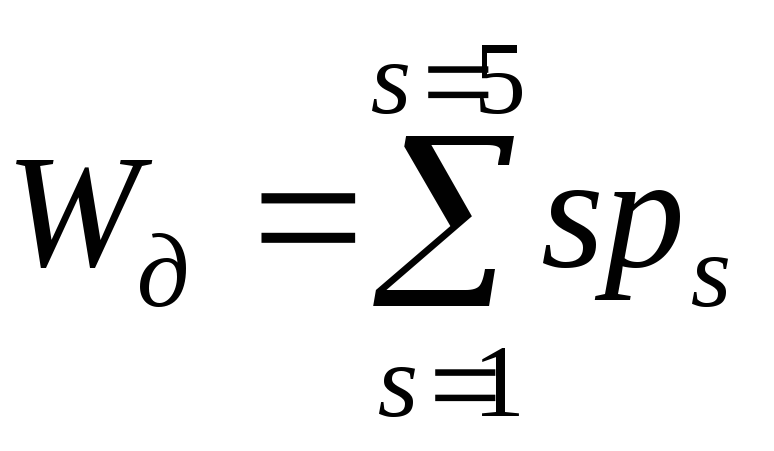 (степень подвижности механизма равна
сумме степеней подвижности всех КП).
(степень подвижности механизма равна
сумме степеней подвижности всех КП).
Однако у механизма может быть большое число звеньев и, следовательно, система уравнений, описывающая такой механизм, будет содержать большое число уравнений. Для того, чтобы упростить анализ сложного механизма, удобно разбить его на более простые модели – структурные группы.
Следует отметить, что рассмотренная модель механизма с жесткими звеньями имеет число степеней подвижности, равное числу степеней свободы. Если модель жесткого звена, входящего в состав механизма, заменить на модель упругого звена, то число степеней свободы увеличится, а число степеней подвижности не изменится. Модели механизмов с упругими звеньями рассматриваются в специальных разделах ТММ и в дисциплине «Колебания в машинах».
Структурная группа – кинематическая цепь, в которой число входов равно числу степеней подвижности (Wц=n). Такое понятие структурной группы было предложено проф. М.З. Коловским. Простая структурная группа – такая, в которой нельзя выделить структурную группу с меньшим числом звеньев. В n-подвижной структурной группе число входов равно n.
В
механизме со структурой «дерева» каждое
звено является структурной группой. На
рис.1.11 можно выделить три структурных
группы (подвижные звенья 2,
3, 4 с соответствующими входными координатами
(q1,
q2,
q3),
так как каждая группа имеет одно звено
(N =
1), одну одноподвижную КП (p1 =
1), один вход (n =
1). Подставляем эти значения в (1.1): 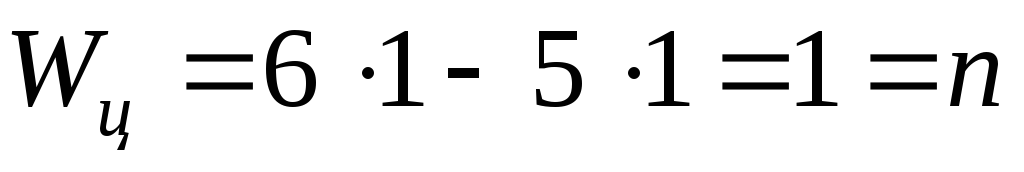 .
.
Структурная группа, как и нормальный механизм, поддается геометрическому анализу. Частным случаем структурной группы является группа, получившая название группы Ассура, в которой число степеней подвижности равно нулю.
Билет №3. Классификация кинематических пар.
М
 одель
подвижного соединения двух звеньев
называется кинематической
парой (КП). Эта модель обладает следующими
свойствами: элементы кинематических
пар считаются недеформируемыми, а
связи, накладываемые кинематической
парой, являются голономными, стационарными
и удерживающими. Важной характеристикой
КП является число степеней свободы s,
которое оставляет КП в относительном
движении соединяемых ею звеньев.
Очевидно, что s
+ k =
6, где k – число связей, накладываемых КП.
Например, если КП оставляет одну степень
свободы в относительном движении (s =
1,
k =
5), то такую пару называют одноподвижной.
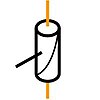
На рис.1.2 представлена вращательная
одноподвижная КП (координата ,
определяющая относительное перемещение
звеньев, является угловой), а на рис.1.3
поступательная
одноподвижная КП (координата х,
определяющая относи
одель
подвижного соединения двух звеньев
называется кинематической
парой (КП). Эта модель обладает следующими
свойствами: элементы кинематических
пар считаются недеформируемыми, а
связи, накладываемые кинематической
парой, являются голономными, стационарными
и удерживающими. Важной характеристикой
КП является число степеней свободы s,
которое оставляет КП в относительном
движении соединяемых ею звеньев.
Очевидно, что s
+ k =
6, где k – число связей, накладываемых КП.
Например, если КП оставляет одну степень
свободы в относительном движении (s =
1,
k =
5), то такую пару называют одноподвижной.
На рис.1.2 представлена вращательная
одноподвижная КП (координата ,
определяющая относительное перемещение
звеньев, является угловой), а на рис.1.3
поступательная
одноподвижная КП (координата х,
определяющая относи тельное
перемещение звенев, является линейной).
тельное
перемещение звенев, является линейной).
 Пример
модели вращательной КП – соединение
ротора двигателя со статором; поступательной
КП – соединение салазок с направляющими.
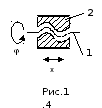
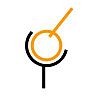
Одноподвижной парой является также и
так называемая винтовая пара,
моделирующая соединение типа «винт-гайка»,
несмотря на то, что в такой паре имеется
два вида относительного движения –
поступательное и вращательное, т.к. два
этих движения не являются независимыми
(рис.1.4).
Пример
модели вращательной КП – соединение
ротора двигателя со статором; поступательной
КП – соединение салазок с направляющими.
Одноподвижной парой является также и
так называемая винтовая пара,
моделирующая соединение типа «винт-гайка»,
несмотря на то, что в такой паре имеется
два вида относительного движения –
поступательное и вращательное, т.к. два
этих движения не являются независимыми
(рис.1.4).
Д вухподвижная пара оставляет две степени свободы в
относительном движении (s=2, k=4).
Это может быть, например, цилиндрическая
пара (рис.1.5), которая допускает
относительное вращательное и поступательное
движение, как в дверной петле. Если в
соединении, моделируемом одноподвижной
КП, одну из деталей рассверлить, то число
степеней свободы в относительном
движении увеличится. Тогда надо
воспользоваться моделью двухподвижной
(рис.1.6, а, б) КП. Трехподвижной парой можно моделировать сферический
шарнир (рис.1.7, а). Иногда число
степеней свободы в сферическом шарнире
ограничивают, устанавливая на внутреннюю
сферу палец и высверливая в наружной
сфере паз; полученное соединение
моделируется двухподвижной КП (рис.1.7, б, в).
вухподвижная пара оставляет две степени свободы в
относительном движении (s=2, k=4).
Это может быть, например, цилиндрическая
пара (рис.1.5), которая допускает
относительное вращательное и поступательное
движение, как в дверной петле. Если в
соединении, моделируемом одноподвижной
КП, одну из деталей рассверлить, то число
степеней свободы в относительном
движении увеличится. Тогда надо
воспользоваться моделью двухподвижной
(рис.1.6, а, б) КП. Трехподвижной парой можно моделировать сферический
шарнир (рис.1.7, а). Иногда число
степеней свободы в сферическом шарнире
ограничивают, устанавливая на внутреннюю
сферу палец и высверливая в наружной
сфере паз; полученное соединение
моделируется двухподвижной КП (рис.1.7, б, в).
Самое большое число степеней свободы в относительном движении, которое может оставить одна КП, равно пяти, так как КП должна накладывать хотя бы одну связь.
 В
некоторых случаях в КП указывается еще
одно свойство. Если у двух звеньев,
входящих в пару, можно построить общие
поверхности, то такие пары называют низшими (например, во вращательной
паре можно построить общий цилиндр, а
в поступательной – общую плоскость). В
противном случае пару называют высшей:
при каждом положении звеньев имеются
только общие линии или точки, расположение
которых меняется в процессе движения
(рис.1.8). Высшей кинематической парой
моделируется, например, соединение двух
зубчатых колес между собой.
В
некоторых случаях в КП указывается еще
одно свойство. Если у двух звеньев,
входящих в пару, можно построить общие
поверхности, то такие пары называют низшими (например, во вращательной
паре можно построить общий цилиндр, а
в поступательной – общую плоскость). В
противном случае пару называют высшей:
при каждом положении звеньев имеются
только общие линии или точки, расположение
которых меняется в процессе движения
(рис.1.8). Высшей кинематической парой
моделируется, например, соединение двух
зубчатых колес между собой.
Ч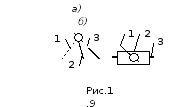 асто
на схеме в одном месте изображают сразу
две кинематические пары. Например, на
рис.1.9, а звенья 1 и 2 образуют
одну вращательную пару, а звено 3 со
звеном 1 или 2 – вторую. На рис.1.9, б также изображены две КП: звено 1 со звеном 2 образует вращательную
КП, а звено 2 со звеном 3 –
поступательную.
асто
на схеме в одном месте изображают сразу
две кинематические пары. Например, на
рис.1.9, а звенья 1 и 2 образуют
одну вращательную пару, а звено 3 со
звеном 1 или 2 – вторую. На рис.1.9, б также изображены две КП: звено 1 со звеном 2 образует вращательную
КП, а звено 2 со звеном 3 –
поступательную.
Билет №4. Образование нормальных механизмов. Структурная формула. Плоские и пространственные механизмы. Примеры.
Нормальным механизмом
называется такой, в котором число входов
совпадает с числом степеней подвижности.
Модель «нормальный механизм» была
предложена проф. М.З.Коловским; она
удобна тем, что поддается геометрическому
анализу. У рассмотренного механизма
(рис.1.11) имеется еще одно важное свойство
– каждое звено соединено с предыдущим
одной КП. В этом случае говорят, что
механизм имеет структуру «дерева».
В этом случае 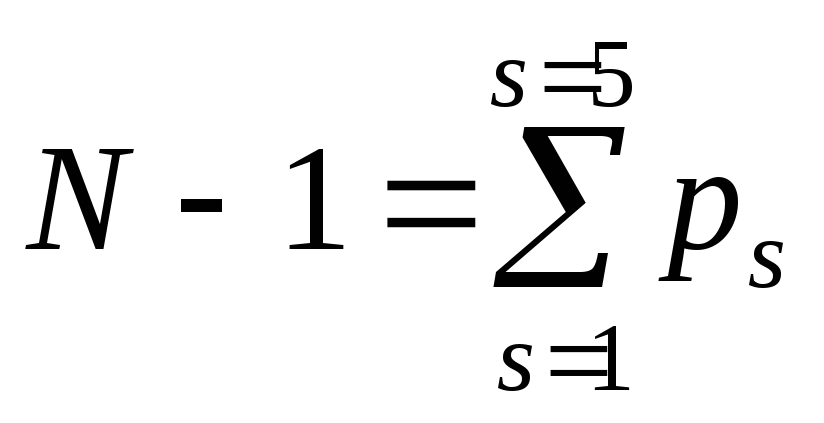 .
.
Рассмотрим примеры. На рис.1.12, а изображено звено, имеющее одну вращательную одноподвижную пару. Число степеней подвижности W=61–51=1. Если задать один вход, обозначенный входной координатой q1, получим одноподвижную группу. Присоединив ее к стойке, получим одноподвижный механизм, состоящий из одного подвижного и одного неподвижного звена (рис.1.12,б).
Н а
рис.1.13 изображен механизм, включающий
в себя, кроме стойки, звенья AB, BC и CD.
Звено AB,
включающее в себя вращательную пару А,
как мы выяснили, является одноподвижной
группой. Оставшиеся два звена BC и CD имеют одну одноподвижную пару D,
одну двухподвижную пару С и трехподвижную пару В;
таким образом, Wц=62–51–41–31=0.
Следовательно, эта цепь является
структурной группой Ассура, а весь
механизм состоит из одной одноподвижной
группы и одной группы Ассура.
а
рис.1.13 изображен механизм, включающий
в себя, кроме стойки, звенья AB, BC и CD.
Звено AB,
включающее в себя вращательную пару А,
как мы выяснили, является одноподвижной
группой. Оставшиеся два звена BC и CD имеют одну одноподвижную пару D,
одну двухподвижную пару С и трехподвижную пару В;
таким образом, Wц=62–51–41–31=0.
Следовательно, эта цепь является
структурной группой Ассура, а весь
механизм состоит из одной одноподвижной
группы и одной группы Ассура.
Н а
рис.1.14 изображена схема платформы
Стьюарта.
В ней N =
14, р1 =
6, р2=6, р3=6.
Следовательно, W=6(14–1)–56–
–46–36=6,
т.е. платформа обладает шестью степенями
подвижности.
а
рис.1.14 изображена схема платформы
Стьюарта.
В ней N =
14, р1 =
6, р2=6, р3=6.
Следовательно, W=6(14–1)–56–
–46–36=6,
т.е. платформа обладает шестью степенями
подвижности.
Наряду с формулой Малышева–Сомова для определения степени подвижности механизма можно воспользоваться методом размыкания:
Размыкаем кинематические пары, преобразуя замкнутую структуру механизма в структуру «дерева».
Группа звеньев является структурной группой, если:
может быть отделена от механизма,
число разомкнутых связей в этой группе равно суммарному числу степеней подвижности пассивных шарниров.
Рассмотрим механизм, показанный на рис.1.13:
Размыкаем шарнир D (5 связей).
Группа звеньев BC, CD является структурной группой, так как
может быть отделена от механизма,
число разомкнутых связей в этой группе (5) равно суммарному числу степеней подвижности пассивных шарниров C (s=2) и B (s=3).
Билет №5 Механизмы с избыточными связями и лишними степенями подвижности. Избыточные связи: освобождающие и неосвобождающие
Р ассмотрим
механизм, показанный на рис.1.15, а.
Его называют шарнирным
четырехзвенником,
так как у него четыре звена, включая
стойку, и все кинематические пары (КП)
являются шарнирами. На реальной модели
видно, что механизм является одноподвижным:
вращая кривошип, мы сообщаем полностью
определенное движение остальным звеньям.
Однако из формулы Малышева–Сомова
(1.2) следует, что число степеней подвижности
механизма отрицательно: W =
6(4 – 1) – 54
= –2, т.е. рассматриваемая схема представляет
собой неподвижную ферму. Очевидное
несоответствие объясняется тем, что мы
подставили в формулу (1.2) и те связи,
которые в реальном механизме не
используются. Их называют избыточными
связями.
Например, в данном механизме все звенья
движутся в параллельных плоскостях,
следовательно, те связи, которые не
позволяют звеньям выйти из плоскости
их движения, не использованы. Такие
связи можно убрать, и при этом число
степеней подвижности механизма не
изменится. Например, вместо одноподвижной
КП можно поставить двухподвижный
цилиндрический шарнир, который позволяет
звеньям выходить из плоскости их
относительного вращения, однако эта
возможность в данном механизме не будет
использована, поскольку нет сил, которые
вынуждали бы звенья выйти из плоскости
их движения. Однако если окажется, что
оси всех шарниров четырехзвенника не
будут строго параллельны друг другу,
то звенья будут стремиться двигаться
уже не в параллельных плоскостях; в этом
случае проявятся избыточные связи,
которые не дадут звеньям провернуться
и превратят механизм в ферму.
ассмотрим
механизм, показанный на рис.1.15, а.
Его называют шарнирным
четырехзвенником,
так как у него четыре звена, включая
стойку, и все кинематические пары (КП)
являются шарнирами. На реальной модели
видно, что механизм является одноподвижным:
вращая кривошип, мы сообщаем полностью
определенное движение остальным звеньям.
Однако из формулы Малышева–Сомова
(1.2) следует, что число степеней подвижности
механизма отрицательно: W =
6(4 – 1) – 54
= –2, т.е. рассматриваемая схема представляет
собой неподвижную ферму. Очевидное
несоответствие объясняется тем, что мы
подставили в формулу (1.2) и те связи,
которые в реальном механизме не
используются. Их называют избыточными
связями.
Например, в данном механизме все звенья
движутся в параллельных плоскостях,
следовательно, те связи, которые не
позволяют звеньям выйти из плоскости
их движения, не использованы. Такие
связи можно убрать, и при этом число
степеней подвижности механизма не
изменится. Например, вместо одноподвижной
КП можно поставить двухподвижный
цилиндрический шарнир, который позволяет
звеньям выходить из плоскости их
относительного вращения, однако эта
возможность в данном механизме не будет
использована, поскольку нет сил, которые
вынуждали бы звенья выйти из плоскости
их движения. Однако если окажется, что
оси всех шарниров четырехзвенника не
будут строго параллельны друг другу,
то звенья будут стремиться двигаться
уже не в параллельных плоскостях; в этом
случае проявятся избыточные связи,
которые не дадут звеньям провернуться
и превратят механизм в ферму.
Механизмы с избыточными связями используют для повышения жесткости конструкции. Однако они накладывают повышенные требования к точности изготовления деталей и их монтажа (в данном случае – требование к соблюдению параллельности осей шарниров), и, следовательно, ведут к удорожанию конструкции. Если эти требования выполнены не в достаточной степени, то для проворачивания механизма нужно прилагать повышенные усилия , что может привести к увеличению трения, повышенному износу, заклиниванию механизма и даже к его поломке. Для того, чтобы избежать этого, в механизмах с непараллельными осями иногда прибегают к рассверливанию отверстий в шарнирах. При этом одноподвижные КП превращаются в двухподвижные (см. рис. 1.15,б). Число степеней подвижности в таком механизме равно: W = 6(4–1)–51–43 =1. Однако в таком механизме появляются зазоры в соединениях, следовательно, падает точность работы механизма; при перемене знака передаваемых усилий в соединении возникает ударная нагрузка на соединения, что приводит к их поломке.
Для того, чтобы определить число избыточных связей q, достаточно вычесть из числа степеней подвижности, найденного опытным путем, число степеней подвижности, найденное по формуле (1.2). В случае шарнирного четырехзвенника это 1 – ( –2) = 3. Формула Малышева – Сомова с учетом избыточных связей имеет вид:
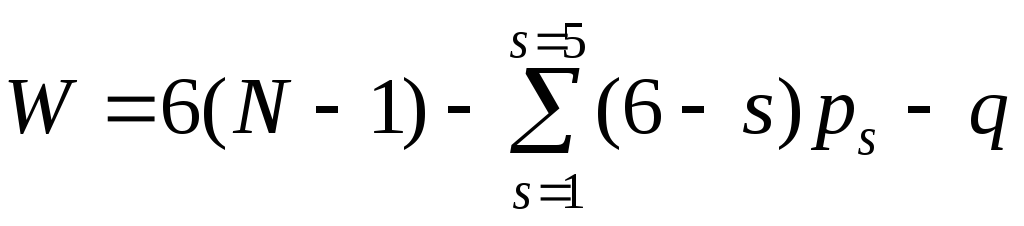 .
(1.2’)
.
(1.2’)
Р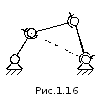 ассмотрим
еще один четырехзвенный механизм,
представленный на рис.1.16. У него один
одноподвижный шарнир и три двухподвижных,
которые допускают относительное вращение
входящих в них звеньев вокруг двух осей,
следовательно, общее число степеней
подвижности равно 1. Однако в некоторых
положениях может оказаться так, что
оси, допускающие относительное вращение
звеньев, у двух несмежных шарниров
совпадут, как показано на рис. пунктирной
линией. Возникнет мгновенная ось
вращения, вокруг которой будут стремиться
повернуться шатун и коромысло. То есть
появилась «лишняя» степень подвижности,
не выявленная формулой Малышева –
Сомова и обусловленная подбором
кинематических пар. Механизм, показанный
на рис. 1.16, носит название механизма
Теннета. В этом механизме возможно
появление «лишних» степеней подвижности,
выраженное вращением шатуна и коромысла
вокруг их продольных осей.
ассмотрим
еще один четырехзвенный механизм,
представленный на рис.1.16. У него один
одноподвижный шарнир и три двухподвижных,
которые допускают относительное вращение
входящих в них звеньев вокруг двух осей,
следовательно, общее число степеней
подвижности равно 1. Однако в некоторых
положениях может оказаться так, что
оси, допускающие относительное вращение
звеньев, у двух несмежных шарниров
совпадут, как показано на рис. пунктирной
линией. Возникнет мгновенная ось
вращения, вокруг которой будут стремиться
повернуться шатун и коромысло. То есть
появилась «лишняя» степень подвижности,
не выявленная формулой Малышева –
Сомова и обусловленная подбором
кинематических пар. Механизм, показанный
на рис. 1.16, носит название механизма
Теннета. В этом механизме возможно
появление «лишних» степеней подвижности,
выраженное вращением шатуна и коромысла
вокруг их продольных осей.
Билет№6. Плоские механизмы и плоские группы Ассура. Формула Чебышева. Класс и порядок группы.
1. Общие сведения о машинах и механизмах: классификация и назначение.
Машина – это устройство для выполнения полезной работы, связанной с производством, транспортировкой, передачей энергии и информации. Благодаря их использованию повышается производительность труда, облегчается физический и умственный труд человека.
По назначению машины условно подразделяются на три группы:
1) энергетические машины, в которых какой-либо вид энергии (электрический, тепловой) преобразуется в механическую работу и наоборот. К этой группе относятся как машины-двигатели (электродвигатели, тепловые и ядерные двигатели), так и машины преобразователи (компрессоры, электрические генераторы).
2) технологические или рабочие машины, преобразующие форму, свойства, положение обрабатываемого предмета (металлорежущие станки, горнодобывающие, транспортные машины).
3) информационные машины, предназначенные для управления технологическими процессами, а также для автоматизации процесса обработки информации и вычислений.
В зависимости от способа управления различают машины ручного управления (на встроенном рабочем месте или дистанционно), полуавтоматического и автоматического действия. Машина, в которой преобразование энергии (материалов и информации) происходит без непосредственного участия человека, называется машиной-автоматом. Совокупность машин-автоматов, соединенных между собой автоматическими транспортными устройствами и предназначенных для выполнения определенного технологического процесса, образует автоматическую линию.
Механизм – часть машины, в которой рабочий процесс реализуется путем выполнения определенных механических движений. Механизм представляет собой систему взаимосвязанных тел, предназначенных для преобразования движения одного или нескольких тел в требуемые движения других тел.
Механизм осуществляет передачу энергии (движения), как правило, с преобразованием сил и характеристик закона движения от источника, например двигателя, к одному или нескольким рабочим органам машины.
Если в преобразовании движения участвуют жидкие или газообразные тела, то механизм называется соответственно гидравлическим или пневматическим. Обычно в механизме имеется одно входное звено, получающее движения от двигателя, и одно выходное звено, соединенное с рабочим органом машины. Существенно, что однотипные механизмы используются в конструкциях самых разнообразных по назначению машин.
2. Основные характеристики и требования, предъявляемые к машинам и механизмам.
Основные характеристики машин: назначение и область применения, способ управления, мощность и производительность, КПД, масса, габаритные размеры, стоимость.
Производительность машин измеряют в единицах, которые наиболее пригодны для обрабатываемого материала. КПД является характеристикой экономичности машин. Он показывает долю полезно реализуемой энергии и эффективность ее использования. Массу и габаритные размеры необходимо знать для транспортирования машин и размещения их на производственных площадях. Основные характеристики машин указывают в их техническом паспорте.
К машинам и механизмам предъявляют следующие требования:
Работоспособность – состояние машин и механизмов, при котором в данный момент времени его основные параметры находятся в пределах, установленных требованиями нормативно-технической документации.
Надежность – способность выполнять заданные функции, сохраняя во времени свои основные характеристики в установленных пределах. Надежность охватывает безотказность, долговечность, ремонтопригодность и сохраняемость. Показатели надежности – вероятность безотказной работы, срок службы и др.
Технологичность. Технологичными называют машины, требующие минимальных затрат средств, времени и труда в производстве, эксплуатации и ремонте.
Экономичность. При оценке экономичности учитывают затраты на проектирование, изготовление, эксплуатацию и ремонт. Экономичность машин достигается за счет снижения материалоемкости, энергоемкости и трудоемкости производства, за счет максимального КПД в эксплуатации при высокой надежности; высокой специализацией производства.
Эргономичность — приспособленность машины к деятельности человека в условиях производства.
2.4. Структура строительной машины
Обязательными составными частями любой технологической, транспортирующей и грузоподъемной машины являются: привод, состоящий из силовой установки, передаточных устройств (трансмиссии) и системы управления; один или несколько рабочих органов и рама (несущие конструкции). У передвижных машин имеется, кроме того, ходовое устройство, соединенное с рамой машины, называемой в ряде случаев шасси.
Преобразование строительных материалов названными машинами происходит в результате движения их рабочих органов, которое сообщается им от силовой установки через трансмиссию. Иногда конечное звено трансмиссии входит в состав сборочной единицы машины вместе с ее рабочим органом. Например, рабочим органом ленточного конвейера служит конвейерная лента, которая приводится в движение от приводного барабана, по существу являющегося конечным звеном трансмиссии, но входящего в состав собственно конвейера (без привода). В подобных случаях конечное звено трансмиссии называют исполнительным механизмом.
Движения рабочего органа могут быть простыми, как, например, вращение лопастного вала растворосмесителя при перемешивании компонентов приготовляемого строительного раствора, и сложными, как, например, движения ковша гидравлического одноковшового экскаватора на разных операциях экскава- ционного рабочего цикла (поворот ковша относительно неподвижной рукояти, поворот рукояти с фиксированным на ней ковшом, одновременный поворот ковша и рукояти и т.д.). Сложное движение рабочего органа есть результат сложения относительного (поворот ковша относительно рукояти) и переносного (поворот рукояти, стрелы, поворотной платформы) движений. Механизмы, обеспечивающие переносные движения, кинематически связаны с рабочим органом и по существу относятся к трансмиссии, но по указанной выше причине их принадлежности к одной с рабочим органом сборочной единице (в данном случае — группе сборочных единиц) они являются исполнительными механизмами. Таким образом, движение рабочему органу может передаваться непосредственно от силовой установки через трансмиссию или через исполнительные механизмы в форме переносных движений.
Примером машины с несколькими рабочими органами может служить траншейный роторный экскаватор, у которого землеройный рабочий орган — ротор приводится в движение от силовой установки через трансмиссию непосредственно, а конвейерная лента транспортирующего рабочего органа — отвалообразовате- ля, кроме того, через исполнительный механизм — приводной барабан.
Для включения в действие машины и ее отдельных механизмов, включая силовую установку, а также для их остановки служит система управления. Структурные схемы машин приведены на рис. 2.1.
Транспортные машины, как правило, не имеют рабочих органов. Взаимодействующие с транспортируемым материалом кузова и платформы этих машин пассивны, а груз перемещается только за счет движения ходовых устройств (рис. 2.2).
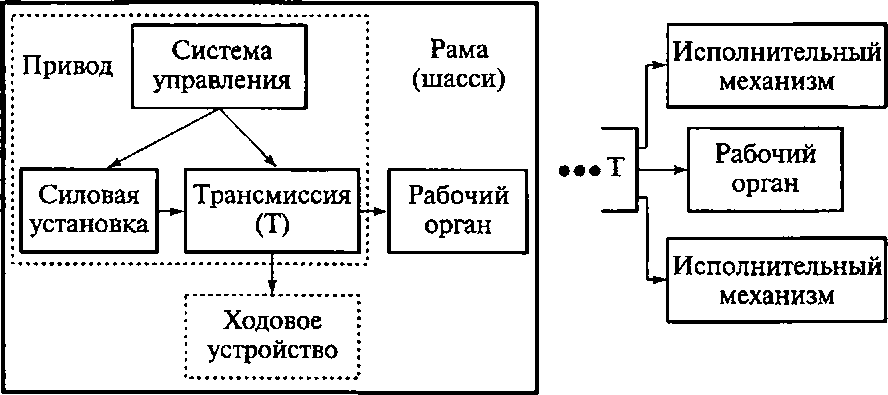
а б
Рис. 2.1. Структурная схема технологической, транспортирующей и грузоподъемной машин при передаче движения рабочему органу через трансмиссию непосредственно (а) и с помощью исполнительных механизмов (б)
Кроме перечисленных обязательных составных частей на машинах могут быть установлены дополнительные (вспомогательные) устройства, например, выносные опоры в конструкциях пневмоколесных кранов, экскаваторов и т. п.
Приводы строительных машин, включающие силовую установку, передаточные устройства и систему управления, а также ходовые устройства обладают конструктивной и функциональной общностью, что позволяет изучать их независимо от видов машин. Вопросы общего устройства и принципа действия этих составных частей машин рассмотрены в гл. 3 — 7.

 одель
подвижного соединения двух звеньев
называется кинематической
парой (КП). Эта модель обладает следующими
свойствами: элементы кинематических
пар считаются недеформируемыми, а
связи, накладываемые кинематической
парой, являются голономными, стационарными
и удерживающими. Важной характеристикой
КП является число степеней свободы s,
которое оставляет КП в относительном
движении соединяемых ею звеньев.
Очевидно, что s
+ k =
6, где k – число связей, накладываемых КП.
Например, если КП оставляет одну степень
свободы в относительном движении (s =
1,
k =
5), то такую пару называют одноподвижной.
На рис.1.2 представлена вращательная
одноподвижная КП (координата ,
определяющая относительное перемещение
звеньев, является угловой), а на рис.1.3
поступательная
одноподвижная КП (координата х,
определяющая относи
одель
подвижного соединения двух звеньев
называется кинематической
парой (КП). Эта модель обладает следующими
свойствами: элементы кинематических
пар считаются недеформируемыми, а
связи, накладываемые кинематической
парой, являются голономными, стационарными
и удерживающими. Важной характеристикой
КП является число степеней свободы s,
которое оставляет КП в относительном
движении соединяемых ею звеньев.
Очевидно, что s
+ k =
6, где k – число связей, накладываемых КП.
Например, если КП оставляет одну степень
свободы в относительном движении (s =
1,
k =
5), то такую пару называют одноподвижной.
На рис.1.2 представлена вращательная
одноподвижная КП (координата ,
определяющая относительное перемещение
звеньев, является угловой), а на рис.1.3
поступательная
одноподвижная КП (координата х,
определяющая относи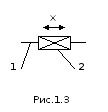 тельное
перемещение звенев, является линейной).
тельное
перемещение звенев, является линейной).